Sie befinden sich hier: Startseite » Erschienene Hefte » Ausgabe Nr. 4 - 2001-2002 » Teaching Nondeterminism as a Special Case of Randomization - 2001
Diese Seite drucken

Teaching Nondeterminism as a Special Case of Randomization

 

Ingo Wegener

FB Informatik, LS2, Univ. of Dortmund,
D-44221 Dortmund, Germany
Email: wegener@ls2.cs.uni-dortmund.de


Abstract:
Nondeterminism is a central concept in computer science. Every student of computer science is faced with this concept, since it is the basis of the NP-completeness theory and is applied in automata theory, formal languages, and many more areas. Students tend to have difficulties with the abstract concept of nondeterminism. Here a different approach to nondeterminism is proposed. Students should first learn the fundamental concept of randomization and randomized algorithms, since randomization has nowadays applications in all areas of computer science. Afterwards, nondeterminism can be easily introduced as a special case of randomization.

Zusammenfassung:
Nichtdeterminismus ist ein zentrales Konzept in der Informatik. Jeder Informatikstudent wird im Laufe seines Studiums mit diesem Konzept konfrontiert, denn es ist die Grundlage der Theorie der NP-Vollständigkeit und wird in der Automatentheorie, bei formalen Sprachen und in vielen anderen Bereichen angewendet. Studenten haben häufig Schwierigkeiten mit dem abstrakten Konzept des Nichtdeterminismus. Wir stellen hier einen anderen Zugang zum Nichtdeterminismus vor. Studenten sollten danach zuerst mit dem grundlegenden Konzept der Randomisierung und mit randomisierten Algorithmen vertraut gemacht werden, denn Randomisierung hat gegenwärtig Anwendungen in allen Bereichen der Informatik. Anschließend kann Nichtdeterminismus als Spezialfall der Randomisierung behandelt werden.


Introduction

Nondeterminism is one of the oldest and most fundamental abstract concepts in computer science. Nondeterministic automata describe the possible behavior of finite-memory computers. Machine models describing the classes of context-free and context-sensitive languages are inherently (or, at least, presumably inherently) nondeterministic. The NP-completeness theory which had influence on the thinking of all computer scientists is based on the complexity class NP of all decision problems which can be decided nondeterministically in polynomial time. Hence, every student of computer science is faced with nondeterminism which usually is defined in the following way.

A nondeterministic machine has the possibility to choose in each configuration its successor configuration from a finite set of configurations. It accepts an input iff there is a legal computation path to an accepting configuration.

The typical question of a student is: "How can we build such a machine?" The typical answer is that a nondeterministic machine cannot be built and that nondeterministic machines are abstract devices. One may have the idea of a machine which "guesses" the "right" successor configuration if there is one. Another idea is to think of a parallel computer where the different computation paths are followed by different processors. However, in order to simulate a nondeterministic machine for a linear number of steps we may need exponentially many processors. In any case, nondeterminism turns out to be "not realizable." I have held much more than thousand oral examinations on this subject and it has turned out that only excellent students do not have difficulties with the concept of nondeterminism.

Also the other well-known descriptions of nondeterminism are not useful in the very beginning. There is a logic-oriented description (using one existential quantifier for a string of polynomial length and a predicate which is decidable in polynomial time, see, e.g., Garey and Johnson (1979)) and a proof-oriented description (there is a proof of polynomial length convincing a polynomial-time verifier iff the input has to be accepted, see, e.g., Mayr, Prömel, and Steger (1998)). All in all, the common approaches to teach nondeterminism have serious drawbacks. Nevertheless, these descriptions of nondeterminism are useful and have to be taught later, but, as we think, not as first approach to nondeterminism.

Here we propose another approach to nondeterminism. It is not claimed that this approach is totally new. It has been mentioned at least implicitly at various places, but it has never been proposed as the first definition of nondeterminism students should see. The approach is to introduce randomized algorithms and then nondeterminism as a special kind of randomization. This approach has not been proposed in the sixties, seventies, or eighties of the last century, since then randomization was not such a fundamental concept in computer science as today. Nowadays, the design of data structures, algorithms, and search heuristics typically leads to solutions based on randomization (see any monograph on new algorithmic concepts). Hence, it is necessary to teach randomization in the basic courses on theoretical computer science.

In Section 2, we briefly discuss why randomization can and should be introduced in basic computer science courses at universities. In Section 3, we describe complexity classes based on randomized computations and introduce the landscape of these complexity classes. In Section 4, we show how this approach leads directly to the concept of nondeterminism as a special case of randomization. We finish with some conclusions and an outlook.

Randomized algorithms

Quicksort is the most important sorting algorithm. The classical quicksort variant is deterministic. Then quicksort is inefficient for certain inputs. It is only efficient if we believe that all input types, i.e., all permutations of sorted sequences, have the same probability to be processed. There is no reason to believe in such an assumption. Randomization is the key to solve the problem. If the pivot element is chosen randomly, quicksort is with very high probability efficient and this holds for each input.

Randomization is the key to efficient and reasonable behavior in many situations. One famous example is game theory. Consider, e.g., the well-known game called scissors-paper-stone. If we are afraid that our opponent is psychologically superior, our only chance not to lose the game (in the long run) is the use of randomized strategies.

Cryptography and, therefore, data protection and the design of digital signatures are not possible without randomization. Keys have to be chosen randomly in order to confuse opponents. The most popular public-key cryptosystems work with very large prime numbers (approximately 500-1000 bits). How can one obtain such random prime numbers? One chooses random numbers and tests whether they are prime. Efficient deterministic primality test algorithms are not known and one uses randomized algorithms. With very small probability, such a test claims that a composite number is prime (false positive). The idea behind this test is the following. Each number smaller than the given number n is a possible witness that n is not prime. More precisely, if n is prime, there is no witness proving that n is not prime. However, if n is composite, at least half of all possible witnesses prove that n is composite (without revealing a proper factor of n). Using results from classical number theory it can be tested efficiently whether m is a witness to prove that n is composite (for details see Motwani and Raghavan (1995)). Some possible witnesses, perhaps 100, are drawn randomly. Either we have found a witness proving that n is composite or we believe that n is prime. If n is composite, the probability, that among 100 random possible witnesses there is no witness is bounded above by 2-100.

Primality testing is such a famous example, since the problem is important, no efficient deterministic algorithm is known, and the randomized algorithm is efficient and has a failure probability which can be accepted in applications.

"There are two principal advantages to randomized algorithms. The first is performance - for many problems, randomized algorithms run faster than the best known deterministic algorithms. Second, many randomized algorithms are simpler to describe and implement than deterministic algorithms of comparable performance" (Motwani and Raghavan (1995)). This is the case when considering randomized skip lists instead of deterministic balanced search trees, the fingerprinting techniques, game tree evaluation, or randomized search heuristics like simulated annealing or evolutionary algorithms. Already this short list of examples proves that students should learn about randomization very early. Complexity theory has the task to describe complexity classes related to randomized algorithms.

Complexity classes based on randomized computations

We have to distinguish decision problems (decide whether the best tour in a TSP instance has a cost of at most c) and the more general class of so-called search problems (compute an optimal tour for a TSP instance) where perhaps many different outputs are correct. We discuss decision problems and use the notation P for the class of all decision problems which can be solved deterministically in polynomial time. For randomized computations, we have to distinguish the following failure types:

  • two-sided error, i.e., we allow false positives (the answer is "yes" although the right answer is "no") and false negatives (the answer is "no" although the right answer is "yes"),
  • one-sided error, i.e., we allow false negatives but no false positives (or vice versa),
  • zero error, i.e., we allow that the algorithm stops without result, all answers have to be correct.

One-sided error makes no sense for search problems. The other two failure types can easily be generalized to search problems. The possibility of stopping without result is only necessary in the zero-error case. In the case of one-sided error the algorithm can produce the answer "no" in the case of not knowing the answer and in the case of two-sided error it can randomly produce an answer.

Which failure probabilities and refusal probabilities (the algorithm stops without result) do we accept? Let q(n) be an upper bound on the failure or refusal probability for inputs of bit length n:

  • two-sided error: it is necessary that q(n)<1/2 (otherwise, we may randomly guess the result),
  • one-sided error: it is necessary that q(n)<1 (otherwise, we may answer "no" without computation),
  • zero-error: again it is necessary that q(n)<1.

We investigate polynomial-time randomized algorithms. Is the parameter q(n) crucial, i.e., is it possible that problems have efficient algorithms with failure probabilities bounded by q(n) but not with failure probabilities bounded by q(n)/2? This is not the case, if q(n) is not very large. With a simple technique called probability amplification it is possible to reduce the failure or refusal probability significantly. This is very easy in the case of zero-error algorithms. We perform m(n) independent runs of the algorithm. If we get an answer in at least one run, we know the correct answer. The new refusal probability is therefore bounded by q(n)m(n). Even if q(n)=1-1/p(n) for some polynomial p(n), m(n)=np(n) and, therefore, polynomially many independent runs reduce the refusal probability to 2-n. Hence, we have to distinguish only two complexity classes for zero-error algorithms:

  • ZPP, where q(n)<=1-1/p(n) for a polynomial p(n) which is equivalent to q(n)<=2-n and, therefore, to refusal probabilities which can be accepted in most applications (ZPP means zero-error probabilistic polynomial time),
  • ZPP*, where q(n)<1, such refusal probabilities cannot be accepted in most applications and ZPP* is an abstract complexity class.

The situation for one-sided error is similar. If at least one run gives the answer "yes", we know that the answer is "yes." Hence, the failure probability for m(n) independent runs is reduced from q(n) to q(n)m(n). Here we consider the complexity class RP (i.e. randomized polynomial time), where q(n)=1-1/p(n) or equivalently q(n)<=2-n, and the abstract complexity class RP*, where q(n)<1. Problems in RP can be solved efficiently enough. Moreover, let coRP (co means complement) and coRP* be the corresponding complexity classes where false positives are replaced with false negatives.

The situation for two-sided error is more difficult. Some runs may produce the answer "yes" while other runs produce the answer "no." Since we only consider the case q(n)<1/2, the answers have a tendency to be correct. Therefore, we take a majority vote, i.e., we answer "yes" if a majority of the runs answer "yes" (ties can be broken arbitrarily). Using Chernoff bounds (see, e.g., Motwani and Raghavan (1995)) it can be proved that polynomially many runs and a majority vote decrease the failure probability from 1/2-1/p(n) for a polynomial p(n) to 2-n. This leads to the complexity class BPP (i.e. bounded-error probabilistic polynomial time), where q(n)<=1/2-1/p(n) or equivalently q(n)<=2-n, and the abstract complexity class BPP*, where q(n)<1/2.

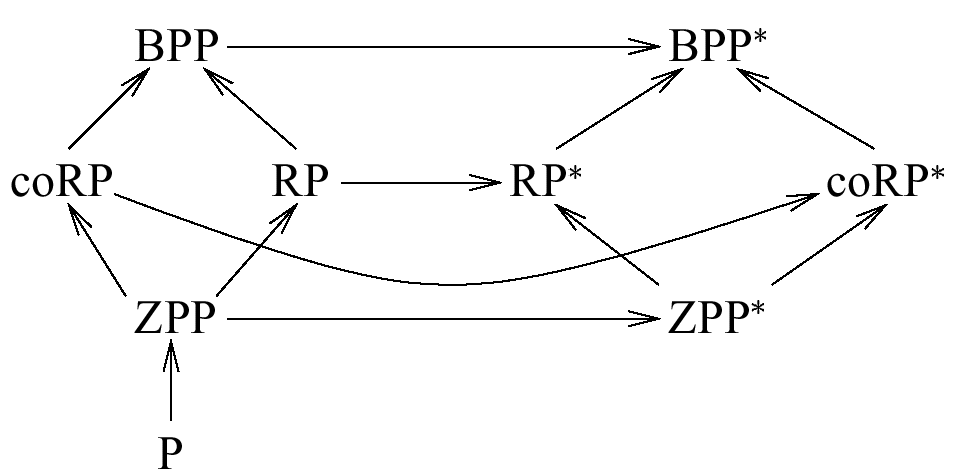
Our considerations lead to the following landscape of complexity classes. A directed edge from A to B corresponds to the relation AB.

Figure 1: The landscape of complexity classes based on randomized computations.

 

All relations in Figure 1 follow from our considerations, only the relation RP*BPP* needs a short proof. The complexity classes on the left side of Figure 1 contain problems which can be solved efficiently, while the complexity classes on the right side seem to be of no practical use. With respect to search problems we obtain a corresponding landscape without RP, coRP, RP*, and coRP*, since one-sided error makes no sense for search problems.

One may argue that this is a long way, before we can introduce nondeterminism. However, we argue that randomized algorithms are of such an importance that students need to know about the different types of randomized algorithms anyway and that, therefore, the landscape of complexity classes based on randomized computations should be taught at the beginning of theoretical computer science.

Nondeterminism is a special case of randomization

Many problems are known to be contained in P. Nowadays, it is still impossible to prove that PBPP*. We look for problems not known to belong to P which are contained in some of the other complexity classes. Primality testing is contained in coRP, since we only accept false positives and the failure probability of a single test is bounded above by 1/2.

Let us consider some decision problems and the decision variants of some well-known difficult optimization problems:

  • knapsack problem, decide whether there is a subset of all considered objects with a total weight bounded above by some parameter W and a total profit bounded below by some parameter B,
  • satisfiability problem, decide whether a circuit has a satisfying input, i.e., an input leading to the output 1 (this is an important problem in hardware verification),
  • traveling salesperson problem, decide whether the cost of some tour is bounded above by some parameter B.

The following RP*-algorithms for these problems work in the same way. In a first step, a possible solution (a choice of a set of objects, a circuit input, or a tour) is randomly chosen. Then it is efficiently and deterministically checked whether this solution fulfills the requirements. The answer "yes" is only given if a legal solution is found. Hence, only false negatives are produced. Moreover, if a solution exists, it is produced with positive probability. These RP*-algorithms have a failure probability which can only be bounded by 1-2-n or 1-1/n! and they are of no practical interest. However, we obtain in a similar way RP*-algorithms for many important problems. This implies that the complexity class RP* is of some theoretical interest.

Indeed, RP* is the complexity class NP!

We reformulate the conditions for RP* algorithms:

  • if the correct answer is "yes", the failure probability is less than 1, i.e., there is a computation path (of positive probability) leading to the correct answer,
  • if the correct answer is "no", the failure probability is 0, i.e., all computation paths lead to the correct answer.

Altogether, the correct answer is "yes" iff there is a computation path (of positive probability) leading to the answer "yes." Computation paths of positive probability can be identified with legal computation paths. Hence, NP-algorithms "are" randomized polynomial-time algorithms with one-sided error allowing false negatives where the failure probability has to be smaller than 1 (which for applications is too large). Nondeterministic algorithms can be realized, although their failure probabilities are too large for serious applications. Nevertheless, nondeterminism is no longer an abstract concept.

Here we can compare the considered randomized algorithms. Randomized quicksort chooses with high probability often good pivot elements. The randomized primality test chooses with high probability among the 100 possible witnesses for the non-primality of n at least one witness. The randomized TSP algorithm chooses only with very small (but non-zero) probability a good tour. However, they all use the principle of random choice.

We discuss one further simple result. If we have for some problem an RP-algorithm A and a coRP-algorithm A', we can run them independently and obtain a ZPP-algorithm A* in the following way:

  • if A answers "yes", we know that "yes" is the correct answer,
  • if A' answers "yes", we know that "yes" is the correct answer for the complementary problem which implies that "no" is the correct answer for the original problem,
  • if A and A' answer "no", one of them has made a failure and A* should refuse to produce an output.

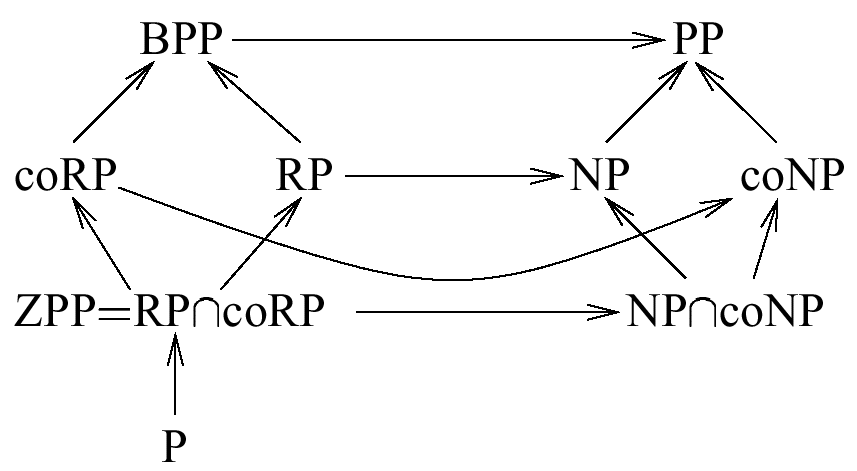
For each input, the refusal probability is bounded by the failure probability of A or A'. This implies that ZPP=RPcoRP and, with the same argument, ZPP*=NPcoNP. Indeed, the notations BPP*, RP*, coRP*, and ZPP* are not used and should be replaced with PP, NP, coNP, and NPcoNP, respectively (PP means probabilistic polynomial time). Figure 2 shows the landscape of Figure 1 with the usual notation.

Figure 2: The landscape of complexity classes based on randomized (and nondeterministic) computations.

Hence, NP and PP belong to the set of complexity classes for randomized computations with an unacceptable failure probability. PP is always considered as a complexity class for randomized computations while NP is usually considered as a complexity class for nondeterministic computations. This proves that it is not a big step to consider NP as a complexity class for randomized computations with an unacceptable failure probability. Our investigations have shown that all considered complexity classes (with the only exception of P) are based on randomized computations. The conclusive distinction is whether the refusal or the failure probability can be made very small, namely 2-n, like for the classes ZPP, RP, coRP, and BPP, or whether these probabilities are too large for applications, like for the classes NPcoNP, NP, coNP, and PP.

Conclusions and outlook

Nondeterministic algorithms are randomized algorithms with one-sided error and a possibly too large failure probability which only has to be smaller than 1. Since randomized algorithms have to be taught anyway, this is a new approach to teach nondeterminism without much extra effort. The main advantage is that nondeterminism is introduced as an algorithmic concept which can be realized on real computers (although the failure probability is too large for real applications).

This new approach has been tested with encouraging success at the computer science department of the University of Dortmund.

The students had the motivation to understand how randomized algorithms work. They learnt how to distinguish practicable randomized algorithms from impracticable ones. However, many important problems only allow impracticable randomized algorithms which turned out to be interesting from a complexity theoretical point of view. After having seen this algorithmic interpretation of nondeterminism the students also learnt the other characterizations of nondeterminism in order to obtain a variety of points of view of this difficult concept. In order to propagate this approach there will be a new textbook entitled "Komplexitätstheorie - ein klassisches Gebiet aus moderner Sicht" ("Complexity theory - a classical field from a modern viewpoint").

References

  • Garey, M.R., and Johnson, D.S. (1979). Computers and Intractability: A Guide to the Theory of NP-completeness. W.H. Freeman.
  • Mayr, E.W., Prömel, H.J., and Steger, A. (Eds.) (1998). Lectures on Proof Verification and Approximation Algorithms. LNCS Tutorial, Springer.
  • Motwani, R., and Raghavan, P. (1995). Randomized Algorithms. Cambridge University Press.

Kommentare

 

^ Top