Information as a Basic Constituent of Human Existence
Engelbert Niehaus
FB Mathematik und Informatik
Universität Münster, Einsteinstr. 62
D-48149 Münster, Germany
Email: niehaus@math.uni-muenster.de
Abstract:
The objective of this article is to use the notion of information as a structuring element in informatics education. Despite of the fact that information is not a constituing element in informatics, this article applies the notion of information as a tool to discover data processing in our environment. Information as a basic constituent of human existence characterizes the meaning of data processing for human beings. This characterization does not depend on the usage of computers. Beyond this the description could be understood as a definition of informatics.
Informatics is the science, which is concerned with information as a basic constituent of human existence.
The acceptance of this definition of informatics implies that the computer is no longer the main object of examination. The definition focusses on basic concepts of data processing concerning human existence. However, these basic concepts do not only become a component of informatics, if they are applied to computer models (like neuroinformatics or DNA-computing). All areas of our environment, in which we can discover and understand data representations and their processing, are of interest for informatics education. In this case the discovery of information in our environment is already a fundamental informatic competence, which could lead to computer models in the next step (but not necessarily).
Zusammenfassung:
Ziel dieses Artikels ist es, den Begriff Information zur Strukturierung von Alltagssituationen in der Didaktik der Informatik zu verwenden. Obwohl der Begriff Information kein konstituierender Begriff in der Informatik ist, so kann der Informationsbegriff zum Entdecken von Datenverarbeitung in unserer Umwelt genutzt werden. Information als ein Grundbaustein menschlicher Existenz charakterisiert die Bedeutung der Datenverarbeitung für uns Menschen unabhängig vom Computer. Darüber hinaus kann diese Sichtweise auf die Didaktik der Informatik auch als Definition verstanden werden:
Informatik ist die Wissenschaft, die sich mit der Information als einem Grundbaustein der menschlichen Existenz auseinandersetzt.
Durch eine solche Definition von Informatik rückt die Bedeutung des Computers als Gegenstand der Untersuchung zunächst in den Hintergrund. Das Ziel ist vielmehr, Grundkonzepte der Datenverarbeitung zu behandeln, die die menschliche Existenz betreffen. Diese Grundkonzepte werden aber nicht erst dann zu einem Bestandteil der Informatikdidaktik, wenn diese, wie z.B. in der Neuroinformatik oder beim Thema DNA-Computing, geeignete Rechnersimulationen hervorgebracht haben, sondern alle Bereiche unserer Umwelt, in denen man Repräsentationen von Daten und deren Verarbeitung entdecken und verstehen kann, sind für die Informatikdidaktik von Bedeutung. Dabei ist das Entdecken des Informationsbegriffs in unserer Umwelt bereits eine fundamentale informatische Kompetenz, die natürlich auch zu Computermodellen führen kann (aber nicht notwendigerweise muss).
1 Ideas and Concepts of Informatics
2 Information: Definitions and Dimensions
4 Fuzziness, Loss of Information and Improvement of Quality
1 Ideas and Concepts of Informatics
In the following section we distinguish between Informatics and Computer Science, characterizing the differences between a computer focused view and the more general perspective on data processing.
The acceptance of the above mentioned definition of informatics affects the half-life of basic informatic ideas and the structure of the subject informatics. E.g. the interhuman communication is one aspect of the above mentioned definition of informatics education. According to the problems and the way, how people communicate with each other, a more general access to the idea of communication is necessary. This broadens the notion of communication which is no longer limited to computer science with aspects like chat, groupware, e-mail, protocol or client server interaction.
If we are concerned with informatics education the above mentioned definition supports the general educational value of lessons in informatics. The main advantage is that the kernel of the education of students and teacher students is less dependent on the technical development of software and computers. So the objective is to reduce the content which is already obsolete after finishing school and university education. This means a prolongation of the half-life of informatic knowledge and applicability of the topics taught in school and university.
From interhuman communication we can derive protocol based technical communication. But beside this aspect interhuman communication is a rich resource to discover, motivate and introduce informatic theories like fuzzy logic (fuzziness of human languages). Furthermore a sociological understanding of interhuman communication is also a decisive point for software development. If developers do not understand, how people communicate with each other independently of technical systems, it is difficult to support communication technically in a way human beings are used to.
Therefore these aspects of general educational value are not relevant for informatics education only, but also for courses considering the conception and the design of software. A more generalized definition of informatics goes beyond the scope of pure Computer Science (=CS). However, this definition of informatics focusses on the borders of CS and embeds the known scopes of CS in a natural way.
Furthermore a consistent realization of the definition would result in restructuring informatics education and a shift of the main focus on the top level, but no existing area of computer science would be excluded from the curriculum. Schwill introduced in [15] the concept of fundamental ideas in informatics (based on Bruner [3]).
Besides the positive influence on half-life of knowledge, a less computer focussed view of informatics leads to a fundamental principle of gaining knowledge and ideas from nature. In our history we often benefit from copying nature's mechanisms and adapting evolutionary processes to technical development (e.g. genetic algorithms). Definitely the growing complexity of today's technical computer based systems demands for mature error correction mechanisms, which ensure the stability of complex technical systems. Ecosystems and our brain are outstanding examples for error correction mechanisms and for handling fuzzy information. The examination of this informatic branch provides insight in a fascinating view on dynamic systems with a deceitful stability of data processing.
Very often people are surprised, that the stability they trusted shows suddenly fundamental changes of behaviour. They do not pay attention to the fact that mechanisms of error correction have only a certain "elasticity". This means that heavy changes of behaviour occur when the mechanism is strained to a point, where the error correction fails.
Also in this case basic concepts of information representation and its processing are examined.
In the following sections we focus on two examples, which show the connection between CS and basic concepts of data processing in informatics.
- Information, Interaction and Complexity:
The Complexity Theory for Algorithms in Computer Sciences (=CS) is extended to the general Complexity Theory. This corresponds to an embedding of the CS-Complexity Theory into general basic informatic concepts for the examination of complex dynamic systems - Application of Information from Art to Image Processing:
An example taken from the field of arts shows, how we can discover fuzzy representations of information in a "uninformatic" looking pencil drawing. Besides the development of the notion "fuzzy" the example can be used to derive a formal definition of fuzziness for informatics education. Hence the example "pencil drawing" serves at the same time as a model for a computer representation of fuzzy data, compression and image processing.
2 Information: Definitions and Dimensions
"Information" is not a constituing notion of informatics, but in this context it serves as a means to analyse systems and to discover data processing in our environment (e.g. learning the mother tongue).Besides the fact that the notion "information" has only accepted definitions for some areas of informatics (Shannon, Information Theory), this notion should help to uncover structures in the first step of problem solving activities (informatics education).
Brockhaus, Naturwissenschaft, Technik[2] describes information as a transfer of data about facts, events and processes between organisms and/or technical systems. According to N.Wiener information defines a third entity besides mass and energy.
If we look at the following figure, we define the notion of information with a bundle of other notions. From an axiomatic point of view "information" is not a notion to start with. But "information" is an important word in our language and it has at least a fuzzy meaning for almost everyone. So using the notion "information" follows the approach: "Start a learning process from what the learner knows".

Figure 1: Information as context dependent mapping of data
The decontextualisation in At1 at a time t1 and contextualisation in Bt2 at t2 includes the loss of data and the distortion of data. Talking about "information" means information about something, so it has the character of a mapping depending on the context the data arises and on the context data is embedded.
Three dimensions of information are defined by C. Floyd [7]:
- personal dimension: the cognition in general and the interpretation of data by human beings.
- organisational dimension: information as a basis for human beings to make decisions.
- medial dimension: information as a storable and transferable entity.
These dimensions of Floyd mix the notion of data with the notion of information. The personal and organisational dimension focusses on the transition and processing (of data) during cognition, interpretation and decisions. This is related to information because transition is a main aspect of the notion. The medial dimension is related to the notion of data as a storable entity. Besides the fact that data can be interpreted as functions/mappings and vice versa we distinguish the following two perspectives:
- Data perspective,
- Information perspective.
From a mathematical point of view the data perspective is related to the notion of elements and sets and the information perspective is related to the notion of evaluating a mapping, i.e. map data in context At1 at time t1 to data in the context Bt2 at time t2.
3 Complexity Theory
Complexity theory in the context of computers is understood as a special branch of Computer Science (CS=Computer Science), estimating the calculation effort of an algorithm depending on the length of an input sequence. This calculation effort can depend e.g. linearly, polynomially, exponentially, ... on the length of an input sequence. Another aspect of CS-Complexity is Kolmogorov Complexity C(s). Let A be an algorithm represented by a sequence of bits. Kolmogorov-Chaitin-Complexity C(s) of a finite binary sequence s is defined to be the length of the shortest algorithm A that with no input outputs s (see [4]). Now we leave the notion of complexity in the context of computer science.
If we accept the introductory definition of informatics, the notion of complexity is too restrictive. Therefore it is necessary to embed the CS-Complexity in a more general notion for examination of complex dynamic systems. Focussing on the general educational value and the discovery of data processing in our environment informatics education can extend CS-Complexity to open childrens'/students' eyes for complexity of dynamic systems in our environment.
The so-called general theory of complexity is an interdisciplinary field of research for the examination and the representation of complex dynamic systems (see [9]). In the following section we try to give a very rough survey.
The theory of complexity contains among other aspects also ideas of meteorology, of economics, of biology with the examination of ecosystems, evolution and behavioural research, of medicine, aspects of cognitive sciences and physics with chaos theory and the examination of subatomic structures. In all areas we deal with basic concepts of data processing according to the introductory definition.
The Nobel prize winner Murray Gell-Mann1 was one of the founders of the Santa Fe Institute2, which exists since 1984 as an interdisciplinary research and education centre, working on a general approach for the examination of complex systems.
In the field of a general theory of complexity, there are meeting different areas of data processing, which are incompatible only on the first sight. As examples we mention the following scopes:
- a bacterium is developing a resistance against an antibiotic,
- customization and modification of an ecosystem following the construction of a beaver dam and resulting changes of flora and fauna,
- learning the mother tongue,
- learning of mathematical structures (not the structures itself),
- creation of a model and its adaption to real-life systems.
In any case we are dealing with processes of adaption and structure formation, for which the behaviour is determined by interaction between external and inner systemic events. In [12] (p.216) Hubwieser mentions the steps for an information centered approach to plan informatics lessons. He describes five steps:
- problem heuristic
- informal problem description
- formal modelling
- realisation and implementation of the solution or simulation
- evaluation.
If lessons in informatics deal with one of the above mentioned settings (e.g. learning the mother tongue), the step "realisation and implementation" is often not possible to realise. Nevertheless the information focused approach is appropriate for the analysis of complex dynamic systems. To determine the interaction between external and inner systemic processes it is necessary to decompose the system into modules (formal modelling). The evaluation is an essential step in making refinements and changes of the formal model. The interaction is based on the notion information as a context dependent mapping between external and internal processes.
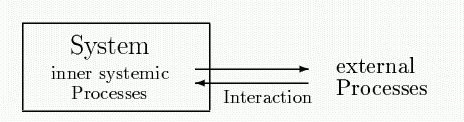
Figure 2: Interaction and modification of inner systemic processes
The interaction between external and inner systemic events implies a change of the internal representation of data. Complex systems often cannot be described completely. Therefore all creations of informatic models are embedded in a steady process of approximation towards the real-life system. Furthermore mechanisms of error correction can also be understood as a way of approximation-to face steady changes of the environment of a considered system.
Adaptive, biological systems, which are successful in the evolution, are characterized by a "suitable" combination of dynamic and rule based aspects of behaviour. On the one hand the rule based aspects are for example necessary for a reliable interaction in social systems, which guarantees stability and on the other hand the adaptability makes it possible to face the steady change of environmental conditions (dynamics). The mechanisms of error correction provides stability and causes at the same time radical and fundamental changes of behaviour when the environmental conditions exceed the elasticity of the error correction mechanism. These changes in the system facilitate the adaption of behaviour to new environmental conditions.
In his article [10] Murray Gell-Mann poses the question:
"What is Complexity?"
This is a guiding question for informatics education starting with different examples of complexity and ending with measurements of algorithmic complexity (see [8]). Informatics education can approach the notion of "complexity" by real-life complex dynamic systems and end up with examples of algorithmic complexity.
According to the introductory definition of informatics we take a closer look on the real-life complex dynamic system. In this case we do not focus on measurement of algorithmic complexity. The skill of analysing a system is the objective for informatics education. The comprehension of complexity can also arise from the analysis of a system and its network of communicating objects.
Depending on the system, the complexity increases by embedding one complex adaptive system into a larger system. This provides a simplified analytic approach to complexity without measurement. In the following step we consider the interaction between embedded systems and the communication inside.
Changes in the system are a consequence of the interaction between external and inner systemic processes. By determining the border of a system we also determine the processes as external resp. internal. Determining the border of a system is part of a modelling process and not necessarily and not naturally given by the real-life system itself.
Looking at system borders the complexity depends on the level of networking between internal and external processes (communication interfaces).
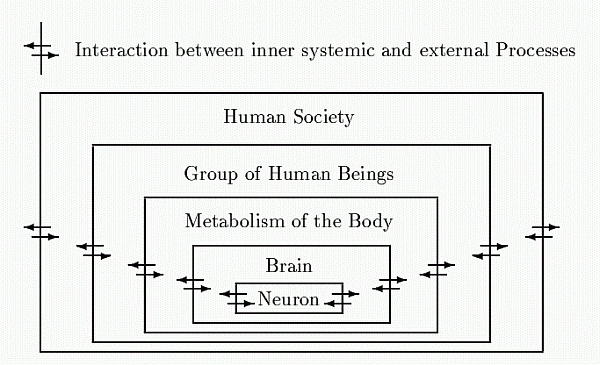
Figure 3: Interaction and growing Complexity
Every neurone is an adaptive dynamic system, which has the possibility to interact with the network environment. The interaction is a process of communication by bioelectrical and biochemical data exchange. The interaction results in changes of the conditions inside the neurone. If we consider the environment of this neurone, a single neurone is embedded in the topology of a neural network with bioelectrical and biochemical communication between the neurones. The complexity of the system does not grow by the number of neurones alone, but also by the topological structure (networking between neurones).
Our brain as an adaptable space with an average number of 10000 connections per neurone. The complexity arises by the high level of connectivity in the topology of the network. The neural network or the central nervous system itself is embedded in the metabolism processes of the complete body. In turn the human being is connected with a group of human beings by communication and non-verbal interactions.
Another step further the social community increases the complexity. The society consists of adaptive dynamic systems (human beings) with a behaviour determined by the individuals and their interactions with each other (process of communication).
The social community is forming an adaptable space. The behaviour of a human being is at the same time the consequence of the group behaviour and the individual behaviour is affecting the group behaviour (networking). Concepts like "tradition" or the "dynamics of group behaviour" are phenomena, which cannot be considered as sums of the behaviours of single human beings. The parallelism of interactions is carrying information and parallel processes are forming the complete meaning of what we call tradition. In terms of computer terminology we can describe the phenomenon as follows:
The hardware, which stores the data, changes and the data migrates between the hardware components. With each migration of data, changes in the stored information are possible. This may happen because of hardware defects or adding resp. losing of context information. The dependence on the environment of the data facilitates that a stable environment stabilizes internal processes.
Looking on computer viruses which can change their shape to aggravate the pattern recognition by virus scanners, for example, adapt this biological concept of migrating and changing information of biological viruses in a simplified way.
If we consider a dynamic system as an adaptive space, the process of self-organization facilitates a mutual modification of adaptive subspaces and the formation of rules or structures. The differences in the given environment characterize the individuality of data processing and its representation (context dependent networking). The notion of context dependency3 of a grammar in CS is also one aspect of context dependency in a more general sense describing in turn aspects of complexity.
These interactions between structure formation (rule orientation) and the individuality are not limited to living nature. The structure of ice crystals is our next example. On the one hand each crystal produces a symmetrical form and on the other hand no crystal is equal to another. Besides this primary system of rules, chaotic aspects and the context dependency of their formation provides the uniqueness of each ice crystal. Also in this case aspects of complexity arise from the analysis of the system. The ice crystal stores environmental information during its formation. The environmental information is encoded in its individual shape. Environmental and inner systemic differences cause the uniqueness of the symmetric shape in the ice crystal.
People can understand language and they can read handwriting although all information has individual characteristic features like the ice crystals. Besides the individual expression of spoken language and handwriting our brain is able to extract the important data. Sejnowski and Rosenberg [17] published an article about an artifical neural network called NETTALK. The content of this article is bridging the gap between the generalized notion of learning a language and the computer science perspective on artifical neural networks.
During the perception of data in the context At1 our brain has to distinguish between important and unimportant data. On the one hand filtering determines the information Bt2 about At1. On the other hand our brain has to generate missing data for information Bt2 about At1 (add context to Bt2). So the information perspective focuses on the analysis with the notion information.
Planning a sequence of lessons in the generalized sense, CS-Complexity is embedded in a broader notion of complexity. When we as teachers work with this generalized notion of complexity the CS-Complexity (e.g. Kolmogorov Complexity) is not the only objective for informatics education. The competence to analyse systems characterizes one key issue of working on complex dynamic systems in schools. According to the steps of Hubwieser in [12] the missing step of realisation and implementation is not a disadvantage for the above mentioned complex dynamic systems. Furthermore it shows that analytic competence is a problem-solving skill which is applicable and useful in settings outside the computer environment.
4 Fuzziness, Loss of Information and Improvement of Quality
Fuzzy representations (representation of blurred data) and context dependency are fundamental aspects of data processing (see [20]). The context dependency is not only closely connected to parallel processing (context generation by parallelism of processes), but also to the fuzzy representation of data. Before we start with an example, we refine the aspects of Figure 1.
If we consider information as a mapping of data from one context At1 to a context Bt2, we can ask the following questions:
- Reversibility: Is it possible to reconstruct the data in context At1 from the data in context Bt2 at a time t3?

Figure 4: Reversibility of a mapping of data
- Reproducibility: Is it possible to produce the data in context Bt2 from At1 again at a different time t3? (e.g. the information f(x) about a number x or the information size of an object x could be reproduced, but information response of a human being on an action x may be difficult to reproduce)
- Quality: Is information Bt2 from At1 helpful, useful, understandable, applicable, ...? Quality is an information about information Bt2 from At1.

Figure 5: Quality as Information about an information
Remark: In many real life situations reproducibility, reversibility and quality are fuzzy notions itself.
Example: (MP3-Compression) Let At1 be an uncompressed audio file and Bt2 be the MP3-compressed audio file with information about At1. The MP3 information Bt2 of At1 is reproducible, because the application of the MP3 algorithm on the audio file will produce the same result (if the same parameters are used). The information is not reversible from Bt2 to At1, because of loss of frequencies (a human being is not able to hear). The quality of Bt2 can be "measured" in different contexts: the file size of Bt2 in comparison to At1 or the loss of frequencies from At1 to Bt2 in the context of frequencies a human being is able to hear. Schwill decribes in [16] informatics as a science of minimal systems with maximal complexity. In this context the example "pencil drawing" (Fig. 6) is related to the aspects:
- Understanding the notion of fuzziness.
- Is it possible to determine relevant and irrelevant information about the original eye (pencil lines define a rough greyscale distribution and not a border of eye features)?
- Is it possible to minimalize the description of the object and keep a maximum of information about the eye?
The following example is chosen from the field of arts to visualize the connection between context dependency and fuzziness. The following quotation of Matisse refers to the introductory definition of informatics, pointing at the fact that the notions of "precision" and "exactness" are not suitable for most types of data processing:
"Precision is Not the Truth." (Henri Matisse)
Considering a simplified naturalistic approach to arts, the painter analyses the environment as exact as possible and tries to produce an exact copy of the reality on the canvas. Being conscious of the fuzziness of most information representations Matisse moves away from the exact description of the human anatomy and simplifies the proportions or their spatial relations.
The way the human eye perceives and processes sensory data indicates a fuzzified decomposition of submodal information4. This leads to an enormous data reduction. This data reduction leads in turn to the fact, that also fuzzy information and their spatial position to each other encodes on a higher visual cortex geometric objects (e.g. lines with a special direction). Detector neurones which react on point patterns with a certain direction do not need a complete line as a visual copy on the retina. For the process of perception only a blurred set of points approximating a line is sufficient for a geometric interpretation as a line with a certain direction.
The following example shows that analytical correctness of the drawn lines is not an indicator that the drawn object can be identified. We can evaluate the quality of the pencil drawing by examining the geometric and perspective correctness.
If we judge with these criteria, we would notice, that hardly any line in the picture is corresponding to a contour of the original.

Figure 6: pencil drawing - July 1999
The pencil drawing in Fig. 6 is an information B about the black&white photo A. The information is not reproducible, because every pencil drawing is unique. The information is not reversible, because it is not possible to reconstruct the black&white photo A from the pencil drawing B.
Our brain is a master in working with fuzzy information. When we compare the contours of the eye or the skin folds we will notice that 90% of all lines in the picture do not correspond to the original eye. This picture is a product of an approximation method. Fuzzy lines do meet the exact contours of the original eye. To approach the original eye more pencil lines were added defining the eye on the paper more precisely.
A single line in the pencil drawing only has small importance. Nevertheless the picture gives a realistic description of an eye, especially when we look at it from a larger distance of approx. 5-6 m.
Now we apply a smoother (soft-focus lens) to the pencil drawing B (Figure 6). The result is drawing C (Fig. 7).

Figure 7: the previous pencil drawing after processing the picture
with a smoother (soft-focus lens) of an image processing program.
A smoother replaces the content of each pixel P1 by the mean of its environment. If we use a 1 Byte encoding of a greyscale pixel, 0 means black and 255 means white.
| 10 | 20 | 170 |
| 20 | 50 | 230 |
| 50 | 150 | 200 |
For every 3x3 submatrix in the whole bitmap the value in the middle of the matrix is replaced by the arithmetic mean of all 9 values of the pixels:
|
|||
The blurred image C (Figure 7) is an information about the pencil drawing B. The information C about B is reproducible, because applying the smoother to B again (with the same parameters) will produce exactly the same image C. The mapping from B to C is not reversible, because we cannot reconstruct the original pencil drawing B from the blurred picture C. In general there is a loss of information from the original black&white-image A to the pencil drawing B and again from pencil drawing B to the blurred picture C. Now we can represent the lines in the pencil drawing by levels of greyscales. As a result this provides the loss of information about the exact contours of the pencil drawing.
We have a loss of information because we can reproduce the greyscale eye by applying the smoother to the pencil drawing again, but we cannot reconstruct the exact position of lines in the pencil drawing from the greyscale picture:
"Improvement of the picture quality despite the loss of information!"
Besides the fact that the greyscale picture has lost information it is more realistic in comparison to the pencil drawing. It has even less dispersions from an original black & white photo. This loss of information is accepted consciously when neural networks are used. If we know that the source data is fuzzy, then it is not necessary to store the complete source data exactly. A mathematical aspect is the conditioned expectation value ([1] Bauer, Wahrscheinlichkeitstheorie, pp. 115, 1991). If we consider the quality aspect and loss of information, we need a formal description of measuring for this aspect. A space ![]() with a
with a ![]() -algebra
-algebra ![]() as a system of measurable subsets of
as a system of measurable subsets of  defines a measurable space (
defines a measurable space ( ,
,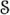 ). Let
). Let ![]() be a
be a ![]() -finite measure on (
-finite measure on (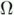 ,
,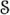 ).
).
A sub-![]() -algebra
-algebra 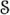 q of
q of 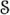 defines the granularity the quality is measured with
defines the granularity the quality is measured with ![]() .
. 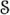 q defines the subset of
q defines the subset of ![]() on which the information has to be preserved. Reducing the amount of sets in
on which the information has to be preserved. Reducing the amount of sets in 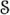 q implies that the information is preserved on fewer sets of
q implies that the information is preserved on fewer sets of 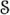 .
.
Application to Pencil Drawing: we do not want to preserve the information of all pixels. We want to preserve the greyscale mean of a 3x3-matrix and we use an information B about A which has less noise in it. So we decompose the image into disjoint 3x3-matrices and store the greyscale means of the matrices. 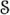 q is the
q is the 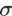 -algebra generated by these 3x3-matrices.
-algebra generated by these 3x3-matrices.
![]()
Figure 8: stored data without interpolation
If we consider the pencil drawing as a piece of art, we have to preserve the information from A to B for all pixels.
That means we take 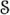 q: =
q: = 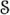 .
.
For two functions A and B, where B is an information about A, preserving the information on 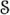 q means:
q means:
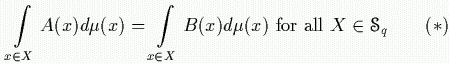
We have a loss of information from A to B for 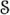 q, if the equality is not true for at least one set X
q, if the equality is not true for at least one set X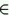
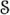 q.
q.
In many cases in order to achieve an efficient representation of data, a loss of information is even desirable (like MP3-compression or noise reduction). In particular we do not always obtain a better representation, if we store the raw data with high precision (pencil drawing) instead of a data reduced fuzzy representation of greyscale by means of the 3x3-matrices. After processing with the smoother this data reduced picture is a better representation of the original eye than the raw pencil drawing. If a loss of information 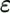 is acceptable on
is acceptable on 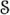 q we extend equality (*) to the following inequality. The
q we extend equality (*) to the following inequality. The ![]() -integrable function
-integrable function ![]() defines the acceptable loss on
defines the acceptable loss on ![]() q:
q:
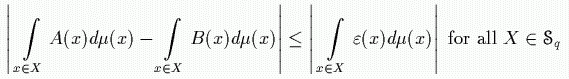
The pencil drawing contains all necessary information for processing the greyscale picture. However, this information is not encoded in shape of the drawn lines, but also in spatial relations between the individual lines and the distribution in the pencil drawing. So a single line gets the final meaning in the context with the other lines.
5 Summary
The two examples from the theory of complexity and from the representation of fuzzy information show that the notion "information" can be used as a tool. With this tool we can broaden informatic ideas (complexity) or we can examine examples outside the computer environment with the perspective of informatics (pencil drawing). In the introductory definition of informatics information is considered a basic constituent in our social, ecological and technical environment. We exclude many aspects from consideration in informatics education, if we focus exclusively on the computer as an object of examination. Besides the hardware of a computer our nature and environment is a rich source of ideas for models in informatics and for the representation and processing of data in the computer.
Restructuring informatics education according to the introductory definition has of course consequences to teaching the content of informatics and the consideration of information as a basic constituent of human existence. If we accept the introductory definition of informatics it requires a certain effort to reorganize our informatic knowledge and embed it into the more general idea of discovery of information in our environment.
The fact that existing contents of informatics education are also completely covered by the introductory definition is not necessarily obvious. Also small steps or partial consideration of the general definition of informatics provide a prolongation of the half-life of the informatic knowledge.
With the notion of information we can consider every discovery outside the computer as a positive expansion of the comprehension of informatics, which could encourage the development or the refinement of computer models.
Not all processes running inside the computer concern informatics, while the notion "information" can help to uncover many processes outside the computer, that embody fundamental ideas in informatics.
References
| [1] | Bauer, H., Wahrscheinlichkeitstheorie, 4. Auflage, de Gruyter, Berlin, New York (1991). |
| [2] | Brockhaus, Naturwissenschaft und Technik, Nachschlagewerk, FA. Brockhaus, Wiesbaden (1983). |
| [3] | Bruner, J.S., The process of education, Camebridge Mass., (1960). |
| [4] | Chaitin, G.J., On the length of programs for computing finit binary sequences, Journal of the Association of Computing Machinery, 13:547-569, (1966). |
| [5] | Deetjen P., Speckmann E.-J., Physiologie, 3. Auflage, Verlag Urban und Fischer (1999). |
| [6] | Edelman, G., Is Neural Darwinism Darwinism?, Winter; 3(1): 41-9 Artificial Life, (1997). |
| [7] | Floyd, C., Informatik - Mensch - Gesellschaft 1. Prüfungsunterlagen, Universität Hamburg, Fachbereich Informatik, October 2001. Zugl.: C. Floyd, R. Klischewski, Informatik - eine Standortbestimmung, Hamburg, September 1998 |
| [8] | Flückiger, M., Rautenberg, M., Komplexität und Messung von Komplexität, Technical Report IfAP/ETH/CC-01/95, ETH Zürich, (1995), http://www.ipo.tue.nl/homepages/mrauterb/publications/COMPLEXITY95paper.pdf, -checked October 15th, 2003- |
| [9] | Gell-Mann, M., Complexity and Complex Adaptive Systems, in J.A. Hawkins and M. Gell-Mann (Hrsg.), The Evolution of Human Languages. SFI Studies in the Sciences of Complexity. Proceedings, Vol. XI, S. 3-18. Reading, MA: Addison-Wesley, (1992). |
| [10] | Gell-Mann, M., What is Complexity? Complexity, Vol. 1, No. 4, S. 9-12 (1995/96). |
| [11] | Griffith, J., Mathematical Neurobiology: An Introduction to the Mathematics of Neurvous System, Academic Press, London, (1971). |
| [12] | Hubwieser, P., Wie soll der Informatikunterricht ablaufen?, in: Informatik und Lernen in der Informationsgesellschaft,Eds.: Hoppe, H.U., Luther, W., Berlin, Heidelberg: Springer Sep. 1997, Informatik aktuell (1997). |
| [13] | Rosch, E., Linguistic Relativity. In Human Communication: Theoretical Explorations, Siverstein, A. L. (Ed.), Halsted Press, New York, (1974). |
| [14] | Rosenfield, I., Neural Darwinism: A New Approach to Memory and Perception, The New York Review of Books, (9. Oktober 1986). |
| [15] | Schwill, A., Fundamentale Ideen der Informatik, Zentralblatt für Didaktik der Mathematik, ZDM 25, 1993, Nr. 1, pp. 20-31, (1993), http://www.informatikdidaktik.de/Forschung/Schriften/ZDM.pdf, -checked: Oktober, 15th 2003- |
| [16] | Schwill, A.., Informatics - The Science of Minimal Systems with Maximal Complexity, p. 17-28, Weert, Tom van, Munro, Robert (Eds.): Informatics and the Digital Society - Proceedings of Conference on Social, Ethical and Cognitive Issues of Informatics and ICT. Norwell, Massachusetts : Kluwer Academic Publishers, (2003), Open IFIP-GI-Conference SECIII, July 22-26, 2002 University of Dortmund, Germany; http://www.informatikdidaktik.de/Forschung/Schriften/SECIII2002/Schwill2002.pdf -checked: Oktober, 20th 2003 |
| [17] | Sejnowski, T. J., Rosenberg, Charles R., NETtalk: A parallel Networks that Learns to Read Aloud, The John Hopkins University Electrical Enginieering and Computer Science Technical Report, JHU/EECS-86/01, (1986). |
| [18] | Thompson, R. F., Das Gehirn von der Nervenzelle zur Verhaltenssteuerung, Heidelberg, (1990). |
| [19] | Winograd, T., und Flores, F., Understanding Computers and Cognition, Norwood, NJ: Ablex Publishing, (1988). |
| [20] | Zimmermann, H.-J.,Fuzzy Set Theory and it Applications, 2ed Kluver Academic Publishers, (1991). |
Footnotes:
1 Murray Gell-Mann was awarded the Nobel prize for physics in 19692 see http://www.santafe.edu
3 context free or context dependent grammar G generating a language L(G).
4 see [5] Deetjen, Speckmann, Physiologie p. 250
Kommentare


