Zeitschrift für fachdidaktische Grundlagen der Informatik

Unterricht - bald nur noch mit Computer?

 

Michael Fothe

Casio-Stiftungsprofessur
Friedrich-Schiller-Universität Jena
Fakultät für Mathematik und Informatik
07743 Jena
fothe@minet.uni-jena.de

 

---

• 1. Einführung
• 2. Zentrale Thesen
• 3. Kommunikation zwischen Schüler und Computer
• 4. Rechnen als Kulturtechnik
• 5. Computer im Mathematikunterricht
• 6. Ziele und Inhalte des Informatikunterrichts
• 7. Zeit- und Speicherverhalten von Quicksort
• 8. Ausblick
• Literatur

---

1. Einführung

Grundpositionen zum Thema stellt der Autor in drei Thesen vor. Dabei beantwortet er u. a. die Frage, ob die Schülerinnen und Schüler an den Schulen künftig von Computern unterrichtet werden sollten. Dann werden Möglichkeiten, Konsequenzen und Probleme des Computereinsatzes im Unterricht anhand von Beispielen aus Mathematik, Informatik und Chemie thematisiert. Als wesentlich wird die Ausgestaltung der Mensch-Maschine-Schnittstelle herausgestellt. Nachfolgend geht es auch um Veränderungen im Mathematikunterricht, um Ziele und Inhalte des Informatikunterrichts und um Kooperation von Mathematik- und Informatiklehrern an Schulen. Das Vorstellen von Aufgaben einer Fachdidaktik und von Forschungsvorhaben rundet die Darlegungen ab.

Dank auch an dieser Stelle an die Casio Europe GmbH für das Stiften der Professur an die Friedrich-Schiller-Universität Jena.

2. Zentrale Thesen

Zur ersten These ist zu sagen, dass die Möglichkeiten derzeit wohl für alle Unterrichtsfächer erschlossen werden. Konzeptionen zum Einsatz von Medien und Werkzeugen im Unterricht sind rechtzeitig zu erarbeiten, um an den Schulen zu agieren und nicht nur zu reagieren. Eine wichtige Frage dabei ist, was mithilfe des Mediums oder Werkzeugs getan wird und was ohne Hilfsmittel zu erledigen ist. Für den Mathematikunterricht soll in dem Zusammenhang auf die Ergebnisse der jährlichen Arbeitstagungen des GDM-Arbeitskreises "Mathematikunterricht und Informatik" und auf die Bücher [13] und [20] verwiesen werden, in denen z. B. das White Box/Black Box-Prinzip beschrieben ist. Auf die vielfältige Literatur zum Lehren und Lernen mit Medien kann hier nur hingewiesen werden (vgl. z. B. [18]). Wegen ihres regionalen Bezugs soll jedoch eine Untersuchung an Thüringer Medienschulen hervorgehoben werden (vgl. [12]). Interviews mit ausgewählten Schülerinnen und Schülern der ersten fünf Medienschulen (derzeit sind es 47 Medienschulen) ergaben das folgende Bild: 75% der Schüler beantworteten die Frage, ob in ihrer Klasse die Lernmotivation durch den Einsatz neuer Medien zugenommen hat, mit Ja. 65% der Schüler sagten, dass die Leistungsbereitschaft der Schüler der eigenen Klasse beim Einsatz neuer Medien spürbar höher ist. Bei den kognitiven Maschinen - siehe zweite These - denke man z. B. an Textverarbeitungssysteme, von denen die Rechtschreibung recht gut und die Grammatik bereits ansatzweise überprüft werden. Solche Systeme sind durchaus hilfreich für Schülerinnen und Schüler (vgl. [2]). Spätestens dann jedoch, wenn kombinierte Diktier-/Textverarbeitungssysteme in den Alltag einziehen, ist die Frage nach der Motivation von Schülerinnen und Schülern zu stellen, das Schreiben ohne moderne Hilfsmittel zu erlernen. Bei der Nachahmung des Menschen im Sinne der künstlichen Intelligenz sind neben Intelligenz auch Bewusstsein und freier Wille zu verlangen (vgl. [4]). Folgerichtig wird in der dritten These nicht dazu aufgerufen, Lehrerinnen und Lehrer durch Computer zu ersetzen. Im Übrigen beträgt das Lehrer-Schüler-Verhältnis an den Thüringer Gymnasien 1 : 15,1 in den Klassenstufen 5-10 und 1 : 11 in den Klassenstufen 11-12. Das Computer-Schüler-Verhältnis ist 1 : 11. Schülerinnen und Schüler der 11. und 12. Klassen treffen mittlerweile also an ihren Schulen auf genau so viele Computer wie auf Lehrerinnen und Lehrer. So weit einige Anmerkungen zu den drei Thesen.

3. Kommunikation zwischen Schüler und Computer

Bei der Entwicklung von pädagogischer Software ist besondere Sorgfalt auf das Ausgestalten der "Schüler-Computer-Schnittstelle" zu legen, was der folgende Dialog deutlich macht:

Für das Ausgestalten der Schnittstelle wird ein Beispiel aus dem Chemieunterricht angegeben: Zu erarbeiten ist ein Programm, das Schülerinnen und Schüler beim Erlernen der chemischen Zeichensprache hilft. Der einfache Vergleich zweier Zeichenfolgen - die korrekte, die im Programm gespeichert ist, und die vom Schüler eingegebene - wäre unzureichend (siehe die weitere Darstellung).

Zuerst wird die formale Sprache der Reaktionsgleichungen für Oxidations- und Redoxreaktionen mittels der erweiterten Backus-Naur-Form (EBNF) definiert:

Zusätzlich werden Kontextbedingungen in verbaler Form hinzugefügt (Symbole, Wertigkeiten, Ladungen usw.). Die Analyse einer Schülerantwort erfolgt in drei Schritten. Im ersten Schritt werden so genannte Eingabefehler erkannt und der Schüler erhält ggf. die Möglichkeit zur Korrektur seiner Zeichenfolge. Wurde die Definition der Eingabesyntax eingehalten, so erfolgt eine interne Übersetzung in die 1. Zwischensprache. Im zweiten Schritt wird überprüft, ob die Syntax der chemischen Zeichen und andere Kontextbedingungen erfüllt sind. Es erfolgt ein Übersetzen in die 2. Zwischensprache. Im dritten Schritt wird die Eingabe des Schülers mit der Vorgabelösung verglichen. Dabei wird versucht, die Schülerantwort nachzuvollziehen. Man spricht von generativen Antwortkontrollverfahren.

Einige Beispiele für Reaktionen des Programms:

Das Vorgehen lehnt sich an übliche Verfahren zur Syntaxanalyse an. Grundlagen für das Programm waren Erfahrungen des Programmautors und empirische Untersuchungen. Das Programm stellt insofern implementierte Lehr-Erfahrung dar. Der Computer kann zum geduldigen und kompetenten Überprüfer von Antworten der Schülerinnen und Schüler werden (vgl. [8]).

4. Rechnen als Kulturtechnik

Breite Volksschichten mussten in den letzten Jahrhunderten, vor allem aus wirtschaftlichen Gründen, das Rechnen erlernen. Dies gelang recht gut, indem Handlungen von deren Bedeutung entkoppelt wurden. Ein Beispiel ist die Multiplikation 4,8 * 26,01. Viele können perfekt multiplizieren und wissen, dass die Teilprodukte versetzt aufzuschreiben sind. Warum das so ist, ist oft unklar. Im täglichen Leben nutzt mittlerweile fast jeder den Taschenrechner und macht sich damit von der Technik abhängig. Die nicht verstandenen Handlungen werden ruhigen Gewissens dem Taschenrechner übertragen. Das Standardbeispiel "Verkäuferin" überzeugt die Schülerinnen und Schüler nicht mehr, das Rechnen ohne Hilfsmittel zu erlernen. Für den Einsatz von Taschenrechnern an Schulen können fünf Forderungen erhoben werden:

Ein Beispiel für grundlegendes Zahlenverständnis: 24 : 0,4 müssen die Schülerinnen und Schüler im Kopf bewältigen. 23,41 : 0,387 können sie dem Taschenrechner überlassen (vgl. [9]). Sicher nicht aus Versehen gab Gottfried Wilhelm Leibniz (1646-1716) seiner Rechenmaschine den Wahlspruch SUPRA HOMINEM. Sie ist also dem Menschen überlegen, was Leibniz damit begründete, dass sie den Menschen durch die Schnelligkeit und Zuverlässigkeit größter Berechnungen übertrifft1.

5. Computer im Mathematikunterricht

Der Einsatz von Tabellenkalkulationen, Computeralgebrasystemen (CAS) und dynamischer Geometriesoftware wird aus didaktisch-methodischer Sicht für den Mathematikunterricht als sehr wünschenswert angesehen (vgl. [11]). Die Computer sollen dabei nicht als Selbstzweck genutzt werden. Vielmehr werden in ihnen Werkzeuge gesehen, mit deren Hilfe Mathematikunterricht verbessert werden kann. Die Notwendigkeit inhaltlicher Verbesserung ist u. a. durch das eher mittelmäßige Abschneiden deutscher Schülerinnen und Schüler bei internationalen Vergleichsuntersuchungen deutlich geworden (vgl. [17]). Ein wichtiges Unterrichtsziel, das nur langfristig zu erreichen ist, ist die Befähigung der Schülerinnen und Schüler zur selbstständigen Auswahl von Werkzeugen, die für eine bestimmte Problemlösung besonders geeignet sind. In den einheitlichen Prüfungsanforderungen der KMK in der Abiturprüfung Mathematik wird dargestellt, dass neue Technologien wirksam eingesetzt werden können bei dynamischen Visualisierungen zum Aufbau von Grundvorstellungen mathematischer Begriffe, als leistungsfähige Werkzeuge bei Modellbildungen und Simulationen sowie zur Förderung heuristisch-experimentellen Arbeitens (vgl. [6]).

Aus dem Alltag weiß man, dass es sinnvoll ist, Aufbau und Arbeitsweise von Werkzeugen zumindest im Prinzip zu kennen. Als Beispiel sei das Auto genannt. Folgerichtig sind Motor und Getriebe Gegenstand von Physik- oder Technikunterricht. CAS können symbolisch differenzieren. Die Zeichenfolge 7x²-5x+3 überführen sie in 14x-5. Die Zeichenfolge x⁴+sin x*x²+2 wird zu 4*x³+sin x*2*x+cos x*x². Für das Werkzeug CAS soll die These formuliert werden, dass Transparenz z. B. durch Programmieren erreichbar ist. Die Kooperation von Mathematik- und Informatiklehrern einer Schule ist dabei sinnvoll. Im Mathematikunterricht werden die mathematischen Grundlagen erarbeitet (z. B. Ableitungsbegriff, Differenziationsregeln, Ableitung spezieller Funktionen). Ein CAS wird im Unterricht vielfältig genutzt. Im Informatikunterricht wird ein Programm erarbeitet, das das symbolische Differenzieren ausführt. Eine geeignete Programmiersprache dafür ist Prolog. Prolog stellt Mechanismen zum automatischen Zerlegen von Zeichenfolgen in ihre Bestandteile unter Berücksichtigung der Vorrangregeln der Operatoren bereit (vgl. [3]). Wir verwenden das dreistellige Prädikat d(F,X,DF). F ist die gegebene Zeichenfolge. DF liefert das Resultat, also die Zeichenfolge, die die 1. Ableitung darstellt. X ist eine Variable für die Variable, nach der differenziert wird. Für spezielle Funktionen werden die folgenden Fakten und Regeln angegeben:

Zum Beispiel bedeutet die fünfte Zeile des Prolog-Programms: Die Zeichenfolge cos (X) wird in die Zeichenfolge -sin(X) überführt. Grafisch lässt sich der Ersetzungsprozess z. B. für die Potenzfunktionen in Anlehnung an die Symbolik bei formalen Sprachen wie folgt darstellen:

Summen- und Produktregel lassen sich in Prolog beschreiben:

Differenz- und Quotientenregel sind entsprechend zu formulieren.

Die Produktregel lässt sich visualisieren:

Grau sind die Funktionen, schwarz deren 1. Ableitungen dargestellt.

Die Kettenregel wird für jede Grundfunktion einzeln angegeben:

DU ist die Zeichenfolge, die der inneren Ableitung entspricht.

Die Kettenregel wird grafisch dargestellt:

Das vollständige Programm besteht nur aus rund 20 Zeilen. Es ist durchaus leistungsfähig, denn sogar mehrfach verschachtelte Funktionen werden von ihm richtig bearbeitet. Die Korrektheit des Ergebnisses ist z. B. bei fünffacher Verschachtelung kaum noch zu überprüfen, da selbst ein geübter Mensch den Überblick über die äußeren und inneren Ableitungen verlieren dürfte. Aus gutem Grund stellen Lehrerinnen und Lehrer in der Schule meistens Aufgaben, bei denen sie die Antworten der Schülerinnen und Schüler korrigieren können.

6. Ziele und Inhalte des Informatikunterrichts

Als geeignete Grundlage für die Konzeption von Informatiklehrplänen und -unterricht haben sich die vier Leitlinien zur informatischen Bildung erwiesen: Interaktion mit Informatiksystemen, Wirkprinzipien von Informatiksystemen, informatische Modellierung sowie Wechselwirkungen zwischen Informatiksystemen, Individuum und Gesellschaft (vgl. [7]). Auf die Expertise zur Entwicklung nationaler Bildungsstandards soll zumindest hingewiesen werden. In ihr werden fünf Kulturwerkzeuge angegeben. Mathematisierungskompetenz und IT-Kompetenz gehören dazu (vgl. [14]). Zur Konsequenz, auch nationale Bildungsstandards für Informatik zu entwickeln, hat dies jedoch (noch?) nicht geführt.

Einfluss auf die künftige Entwicklung des Informatikunterrichts dürften die einheitlichen Prüfungsanforderungen der KMK in der Abiturprüfung Informatik (EPA Informatik) gewinnen, schließlich beschreiben sie die Anforderungen und damit die Kompetenzen, über die die Abiturienten am Ende ihrer Schulzeit verfügen sollen (vgl. [5]). Die EPA Informatik wurden auf der Grundlage der derzeit geltenden Informatiklehrpläne der 16 Länder erarbeitet. Themen, die den Lern- und Prüfungsbereichen der EPA Informatik nicht zuzuordnen sind, können bis zu einem Drittel einer Prüfungsaufgabe ausmachen. Durch diese Öffnung war es nicht notwendig, alle Themen, die in den Ländern derzeit unterrichtet werden, in die EPA aufzunehmen. Damit war es bei deren Erarbeitung möglich, inhaltliche Schwerpunkte zu setzen. Die Entwicklung der Schulinformatik wird vermutlich auch weiterhin dynamisch verlaufen. Die EPA wurden daher so formuliert, dass es nicht erforderlich ist, sie alle drei Jahre zu überarbeiten. Andernfalls wäre der Wert des Faches Informatik für die Allgemeinbildung kritisch zu hinterfragen. EPA legen auch fest, welchen Schwierigkeits- und Komplexitätsgrad Abituraufgaben haben sollen. Diese Festlegungen haben sowieso längerfristigen Bestand. Die EPA Informatik betonen, der fachdidaktischen Diskussion der letzten Jahre folgend, das Modellieren im Informatikunterricht. So werden als grundlegende Modellierungstechniken im Sinne von Techniken der geistigen Arbeit objektorientierte Modellierung, Datenmodellierung, zustandsorientierte Modellierung, Modellierung von Abläufen mit Algorithmen, funktionale Modellierung und regelbasierte Modellierung konkret aufgeführt.

Das Verhältnis von Modellieren und Programmieren betrachtet der Autor als noch nicht ausdiskutiert. Nach seiner Auffassung geht es im Informatikunterricht sowohl um das eine als auch um das andere. H. Wedekind forderte im Rahmen seines Lehrauftrags "Informatik als Grundbildung" im Sommersemester 2004 in Jena, Sprache und Logik als Grundlagen des Informatikunterrichts anzusehen². Dieser Ansatz ist es Wert, auf seine schulische Umsetzbarkeit näher untersucht zu werden (vgl. [19]).

Immer wieder wird nach den für den Einsatz an allgemein bildenden Schulen am besten geeigneten Programmiersprachen gesucht. Ich bezeichne die Suche als das Programmiersprachenproblem und wundere mich - ich gebe gern zu, dass ich hier etwas übertreibe -, dass noch niemand vorgeschlagen hat, die Standards, Systeme und Sprachen HTML, WWW, CSS1, CSS2, DSSSL, XSLT, XSL, CGI, SSI, JSP, ASP, SSJS, PHP, EJB, SSL, DOM Level 1, XML, DTD, XML Schema, XPath, XHTML, XLink, XPointer, Unicode, CORBA, Java, C# und JOSH der Reihe nach im Informatikunterricht abzuhandeln. Kaum ein Lehrer (vermute ich) wäre dazu zwar in der Lage, die Schüler würden daher scharenweise weglaufen, aber modern wäre das Vorgehen allemal. Bei den Diskussionen wird häufig vergessen, dass es nicht Aufgabe von allgemein bildenden Schulen ist, direkt und unmittelbar auf das Berufsleben vorzubereiten. Als Konsequenz sind Kriterien aufzustellen, anhand derer eine Einschätzung von Programmiersprachen erfolgen kann. Dazu soll ein Vorschlag unterbreitet werden:

Mit Interesse las der Autor vor 15 Jahren einen Aufsatz des österreichischen Computerpioniers H. Zemanek über das Prinzip LOOK! (vgl. [21]). Ein Beispiel für LOOK! liefert die folgende Abbildung, die in der Topic Study Group 16 (Visualisation in the teaching and learning of mathematics) von ICME-10 präsentiert wurde (4.-11. Juli 2004 in Kopenhagen):

 

An der Abbildung lässt sich der Wert der entsprechenden unendlichen geometrischen Reihe ? + (?)² + (?)³ + (?)⁴ + (?)⁵ + … ablesen. (Die Lösung wird hier nicht verraten.)

In dem Zusammenhang kann die Studienarbeit von L. Kohl genannt werden, in der es um visuelle Programmiersprachen für den Einsatz an Schulen geht. In der Arbeit wurden existierende Systeme analysiert, es wurden Informatik-Lehrkräfte zu ihren Erfahrungen und Vorstellungen zu dem Thema interviewt und es wurden Anforderungen an eine visuelle Programmiersprache für den Einsteiger spezifiziert (vgl. [15]). In der darauf aufbauenden Diplomarbeit werden Design und Implementierung des Systems "Puck" vorgestellt und es wird über erste Erfahrungen bei dessen Einsatz an Schulen berichtet. Ein visuelles Programm wird aus Bausteinen zusammengefügt, die formschlüssig ineinander passen. Zahlreiche Fehlermöglichkeiten sind damit ausgeschlossen. Aus dem visuellen Programm wird der Quelltext automatisch generiert (exemplarisch in Oberon-2). Das folgende mit Puck entwickelte Programm löst das bekannte Problem "Türme von Hanoi":

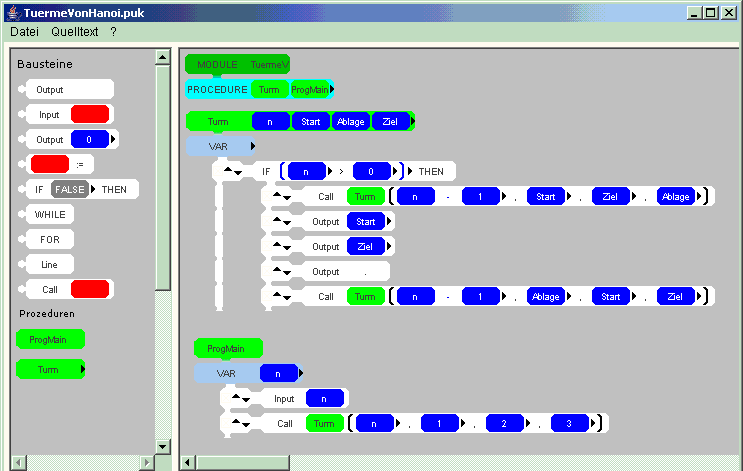
7. Zeit- und Speicherverhalten von Quicksort

Die zentrale Fragestellung einer Fachdidaktik lautet: Was soll warum, wann, wie und mit welchem Ziel gelehrt werden? W. Lütgert wies darauf hin, dass die Jenaer Didaktik-Tradition seit ihren Anfängen unter dem Gedanken der Verbindung von Theorie und Praxis steht, ohne die Differenz der Bereiche Profession und Disziplin zu verwischen: Lehrkunst auf der einen Seite und Wissenschaft von der Lehrkunst auf der anderen Seite (vgl. [16]).

Auf die Frage "Wo ist eigentlich das Problem?" sollen drei Antworten gegeben werden: Komplexität des Denkens, Komplexität des Unterrichts und der populäre Irrtum "Das Lehren-Können kommt schon von allein". Eine Aufgabe der Fachdidaktiken ist das Entwickeln und Erproben von Unterrichtsszenarien. In diesem Abschnitt wird das Thema "Zeit- und Speicherverhalten von Quicksort" näher dargestellt. Dabei erfolgt eine Bezugnahme auf eine Veröffentlichung des Autors, in der das Thema aus der Perspektive des entdeckenden Lernens aufbereitet wurde, wobei Phänomene beobachtet und dann erklärt werden (vgl. [10]). Nachfolgend wird eine Anregung von R. Baumann aufgegriffen und die experimentelle Methode angewandt (vgl. [1]). Aus Gründen der Konzentration auf das Wesentliche werden stets nur Zahlen sortiert (Datentyp REAL). Die Problemgröße ist die Anzahl n an Zahlen. Nachfolgend wird vorausgesetzt, dass die Leserin oder der Leser wissen, wie Quicksort funktioniert.

Zu Beginn werden Hypothesen für das Zeitverhalten von Quicksort im besten und schlechtesten Fall erarbeitet. Dafür wird ein einfaches Modell verwendet. Zuerst wird der beste Fall bearbeitet. Zu sortieren ist eine Teilfolge von k Zahlen. Dafür werden erst einmal näherungsweise k Zeiteinheiten benötigt. (Jede Zahl wird mit dem Trennelement verglichen. Manchmal werden zusätzlich zwei Zahlen getauscht.) Dann werden die linke und die rechte Teilfolge in gleicher Weise bearbeitet. Im besten Fall wird eine Teilfolge stets in zwei gleich große Teilfolgen zerlegt. In der Abbildung wird die Situation für 16 Zahlen, die zu sortieren sind, dargestellt. Das Zeichen  steht für eine Zahl und damit nach den Erläuterungen für eine Zeiteinheit. Die Zeichen lassen sich zu einem Rechteck zusammenschieben. Die Fläche als Maß für die benötigte Zeit zum Sortieren von 16 Zahlen hat den Inhalt 16*4. Durch weitere Beispiele lässt sich die Hypothese finden, dass die benötigte Zeit im besten Fall proportional zu n*ld n ist.

 

Nun wird der schlechteste Fall untersucht. Dieser liegt zum Beispiel dann vor, wenn als Trennelement stets die größte Zahl einer Teilfolge genommen wird. Es entsteht ein Dreieck, das den Flächeninhalt 135 besitzt (vgl. nachfolgende Abbildung). Allgemein beträgt der Flächeninhalt (n²+n-2)/2. Die Hypothese lautet: Im schlechtesten Fall ist die benötigte Zeit proportional zu n².

Im Modell werden die Vergleiche präzise berücksichtigt. Die Bewegungen werden dagegen sehr großzügig betrachtet. Diese Vereinfachung ist im Sinne einer Plausibilitätsbetrachtung akzeptabel.

Die Funktionen f und g mit f(x)=x² und g(x)=x*ld x werden jetzt näher analysiert. Was passiert, wenn sich der x-Wert verdoppelt? Bei der Funktion f ergibt sich die Vervierfachung des y-Wertes. Für die Funktion g gilt, dass sich der y-Wert nur auf das (2*(1+1/ld x))-fache vergrößert. Diese Funktion wollen wir daher als "fast linear" bezeichnen. Die beiden Hypothesen für das Zeitverhalten im besten und schlechtesten Fall werden nun experimentell mithilfe von Zeitmessungen überprüft, was auch gelingt.

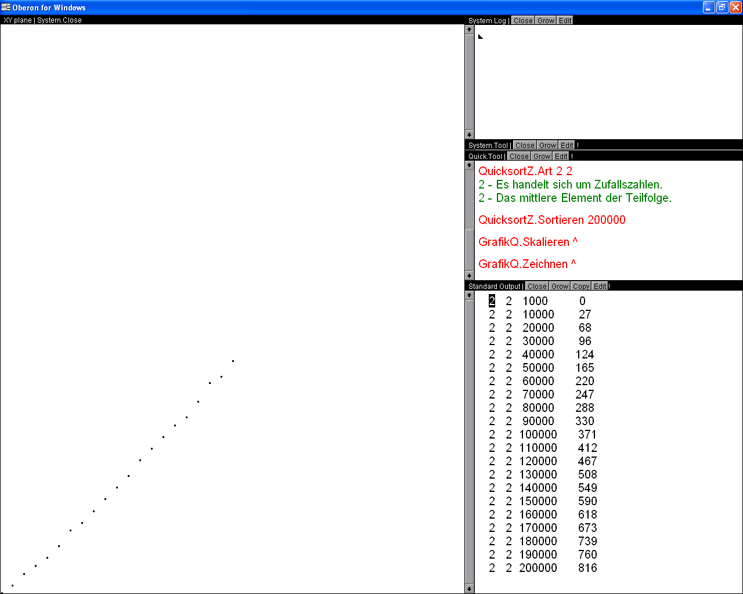
Die nächste Abbildung stellt Messergebnisse für bis zu 200.000 Zufallszahlen dar. Als Trennelement wird jeweils das mittlere Element einer Teilfolge genommen (Abszissenachse: Anzahl an Zahlen, Ordinatenachse: benötigte Zeit).

Abschließend werden zwölf Fälle systematisch untersucht, die sich ergeben aus:

drei möglichen Eigenschaften der gegebenen Zahlen: die Zahlen liegen bereits aufsteigend sortiert vor, es sind Zufallszahlen oder sie liegen falsch herum, also absteigend sortiert vor und vier Möglichkeiten für die Wahl des Trennelementes: es wird stets das erste, das mittlere, das letzte bzw. ein zufälliges Element einer jeden Teilfolge genommen.

Jedes Mal sind z. B. 20.000 Zahlen zu sortieren. Vermutungen über die benötigte Rechenzeit werden aufgestellt und anschließend experimentell überprüft. Aus den Untersuchungen lässt sich ableiten, dass Quicksort meist sehr schnell ist. Langsam ist das Verfahren, wenn die gegebenen Zahlen aufsteigend oder absteigend sortiert sind und wenn als Trennelement stets das erste oder das letzte Element einer Teilfolge genommen wird. Es lässt sich z. B. herausarbeiten, dass der schlechteste Fall auch beim Sortieren von Zufallszahlen und Auswählen von zufälligen Trennelementen eintreten kann, dass dies jedoch sehr unwahrscheinlich ist.

Das oben angegebene Modell eignet sich auch für das Ermitteln des Speicherverhaltens, denn jede Folge von Zeichen  entspricht einem Prozeduraufruf. Im besten Fall liegen gleichzeitig bis zu ld n Einträge im Stapelspeicher vor. Im schlechtesten Fall sind es n-1 Einträge.

8. Ausblick

Ein Schwerpunkt der Forschung im Rahmen der Casio-Stiftungsprofessur soll das Lehrerhandeln im Informatik- und Mathematikunterricht sein. An fünf Gymnasien wird das folgende Szenarium zur externen Unterstützung der Informatiklehrerinnen und -lehrer erprobt: Erarbeiten der Kompetenzbeschreibung für ein Thema, Erstellen von Testaufgaben, Übergabe der Testaufgaben an interessierte Schulen, Schreiben und Auswerten des Tests durch die unterrichtenden Lehrkräfte, Erarbeiten von Schlussfolgerungen für den eigenen Unterricht durch die beteiligten Lehrerinnen und Lehrer. Die eigentlichen Testergebnisse sind durch die Schulen nicht weiterzumelden. Vielmehr werden die Lehrerinnen und Lehrer zu Nutzen, Aufwand, Problemen und Varianten des Vorgehens befragt. Konkreter Gegenstand ist das Thema "Rekursion und Iteration", das Relevanz für die Abiturprüfung im Fach Informatik besitzt (vgl. [5]). Die Untersuchungen stellen einen fachspezifischen Beitrag in der aktuellen Diskussion zu Bildungsstandards dar.

Ein Mathematiklehrer untersucht derzeit die Planungsphase eines Mathematikunterrichts mit CAS genauer. Er ist jeweils zur Hälfte an der Universität und an einem Gymnasium tätig. Dies ist eine Möglichkeit, Schulbezogenheit in der fachdidaktischen Forschung zu gewährleisten. In den Untersuchungen wird von der These ausgegangen, dass der Prozess der Entwicklung der Professionalität der Lehrenden unterstützt werden kann, indem man die Bereitschaft und die Kompetenz zu selbstkritischer Arbeit und zu kommunikativer, kooperativer und öffentlich wirksamer Arbeit befördert (vgl. [11]). Wesentliche Grundlage für die wissenschaftliche Arbeit sind vielfältige eigene Unterrichtserfahrungen.

Und zum Abschluss die schlichte Antwort auf die Frage "Unterricht - bald nur noch mit Computer?": Ja.

Vielen Dank an Christiane Topp; sie erstellte diese Online-Version des Artikels.

Literatur

1.	Baumann, R.: Zeitaufwand von Sortierverfahren. In: LOG IN Heft Nr. 130 (2004), S. 51-55
2.	Berndt, E.-B.: Interaktion mit digitalen Rechtschreibhilfen: ein Vergleich von Schülertexten; neue Wege zur Förderung der Rechtschreibkompetenz in der Sekundarstufe I. Bremen, Univ., Diss. 2002
3.	Clocksin, W. F.; Mellish, C. S.: Programmieren in Prolog. Springer Berlin, Heidelberg, New York 1990
4.	Dietz, P.: Menschengleiche Maschinen. Wahn und Wirklichkeit der künstlichen Intelligenz. Bühler und Heckel Berlin 2003
5.	Einheitliche Prüfungsanforderungen in der Abiturprüfung Informatik. Beschluss vom 1.12.1989 i. d. F. vom 5.2.2004. Luchterhand München, Neuwied 2004
6.	Einheitliche Prüfungsanforderungen in der Abiturprüfung Mathematik. Beschluss vom 1.12.1989 i. d. F. vom 24.5.2002. Luchterhand München, Neuwied 2003
7.	Empfehlungen für ein Gesamtkonzept zur informatischen Bildung an allgemein bildenden Schulen. GI-Fachausschuss "Informatische Bildung in Schulen". Beilage von: LOG IN 20 (2000) Heft 2
8.	Fothe, M.: Antwortkontrollalgorithmen für Reaktionsgleichungen der anorganischen Chemie. In: Dresdner Reihe zur Forschung 15/1986, S. 132-137
9.	Fothe, M.: Rettet, was zu retten ist! In: LOG IN 20 (2000), Heft 6, S. 72
10.	Fothe, M.: Zeitverhalten von Sortierverfahren - Beispiele für experimentelles Arbeiten im Informatikunterricht. In: Hubwieser, P. (Hrsg.): Informatische Fachkonzepte im Unterricht. 10. GI-Fachtagung Informatik und Schule INFOS 2003. Lecture Notes in Informatics, Bonn 2003, S. 111-120
11.	Fothe, M. (Hrsg.): Mathematikunterricht und Computer - Bestandsaufnahme und Ausblick. Bericht von der Tagung am 24./25. September 2004. In: Jenaer Schriften zur Mathematik und Informatik 11/04
12.	Frindte, W.; Stauche, H.: Abschlussbericht zur wissenschaftlichen Begleitung der TSCN-Medienzentren (Kurzfassung). FSU Jena 2004 (Institut für Psychologie, Institut für Erziehungswissenschaften)
13.	Heugl, H.; Klinger, W.; Lechner, J.: Mathematikunterricht mit Computeralgebra-Systemen. Addison-Wesley Bonn, Reading 1996
14.	Klieme, E. u. a.: Zur Entwicklung nationaler Bildungsstandards. Eine Expertise. BMBF 2003
15.	Kohl, L.: Konzepte der visuellen Programmierung und ihrer Einsatzmöglichkeiten an Schulen. Studienarbeit an der FSU Jena 2004 (Fakultät für Mathematik und Informatik)
16.	Lütgert, W.; Hallpap, P. (Hrsg): Didaktik in Jena. Aufgaben zu Beginn des 21. Jahrhunderts. Zentrum für Didaktik Jena 2002
17.	PISA-Konsortium Deutschland (Hrsg.): PISA 2003. Der Bildungsstand der Jugendlichen in Deutschland - Ergebnisse des zweiten internationalen Vergleichs. Waxmann Münster, New York, München, Berlin 2004
18.	Strittmatter, P.; Niegemann, H.: Lehren und Lernen mit Medien. Eine Einführung. Wissenschaftliche Buchgesellschaft Darmstadt 2000
19.	Wedekind, H.; Ortner, E.; Inhetveen, R.: Informatik als Grundbildung, Teil III: Gleichheit und Abstraktion. Informatik Spektrum 4/2004, S. 337-342
20.	Weigand, H.-G.; Weth, T.: Computer im Mathematikunterricht. Neue Wege zu alten Zielen. Spektrum Akademischer Verlag Heidelberg, Berlin 2002
21.	Zemanek, H.: Der Geist in der Flasche: Warum der Computer nicht ausschaut. In: Informationstechnik - it Heft 1/1988, S. 3-10

Kommentare

 

---