To CNF or not to CNF? An Efficient Yet Presentable Version of the CYK Algorithm
Martin Lange, Institut für Informatik
Hans Leiß, Centrum für Informations- und Sprachverarbeitung
Ludwig-Maximilians-Universität München, Germany
martin.lange AT ifi.lmu.de
leiss AT cis.uni-muenchen.de
Abstract:
The most familiar algorithm to decide the membership problem for context-free grammars is the one by Cocke, Younger and Kasami (CYK) using grammars in Chomsky normal form (CNF). We propose to teach a simple modification of the CYK algorithm that uses grammars in a much less restrictive binary normal form (2NF) and two precomputations: the set of nullable nonterminals and the inverse of the unit relation between symbols.
The modified algorithm is equally simple as the original one, but highlights that the at most binary branching rules alone are responsible for the O(n3) time complexity. Moreover, the simple transformation to 2NF comes with a linear increase in grammar size, whereas some transformations to CNF found in most prominent textbooks on formal languages may lead to an exponential increase.
Zusammenfassung:
Der bekannteste Algorithmus für das Wortproblem bei kontextfreien Grammatiken stammt von Cocke, Younger and Kasami (CYK) und verwendet Grammatiken in Chomsky Normalform (CNF). Wir schlagen vor, statt des bekannten Algorithmus einen leicht modifizierten CYK-Algorithmus zu lehren, der Grammatiken in der weniger eingeschränkten binären Normalform (2NF) mit zwei Preprocessing-Schritten verwendet: die Menge der löschbaren Nichtterminalsysmbole und das Inverse der Einheitsrelation zwischen Symbolen.
Der modifizierte Algorithmus ist genauso einfach wie das Original, betont aber, daß die höchstens binären Verzweigungsregeln allein für die Zeitkomplität von O(n3) verantwortlich sind. Darüber hinaus sorgt die einfache Transformation nach 2NF für eine nur lineare Vergrößerung der Grammatik, wohingegen einige Transformationen nach CNF, die man in den meisten bekannten Lehrbüchern über Formale Sprachen findet, für ein exponentielles Wachstum sorgen.
- 1 Introduction
- 2 The CYK Algorithm in Textbooks
- 3 Preliminaries
- 4 The Word Problem for Context-Free Languages
- 5 Conclusion
1 Introduction
The membership and parsing problems for context-free languages (CFL) are of major importance in compiler design, bioinformatics, and computational linguistics. The algorithm due to Cocke [4], Younger [24] and Kasami [9], often called the CYK algorithm, is the most well-known and therefore commonly taught algorithm that solves the word problem for context-free grammars (CFG), and with a minor extension, the parsing problem as well. It is also a very prominent example for an algorithm using dynamic programming, a design principle for recursive algorithms that become efficient by storing the values of intermediate calculations. It is therefore fair to say that the CYK algorithm is one of the most important algorithms in undergraduate syllabi for students in subjects like computer science, (bio)informatics, and computational linguistics.
One would expect that textbooks and course notes reflect this importance by good presentations of efficient versions of CYK. However, this is not the case. In particular, many textbooks present the necessary transformation of a context-free grammar into Chomsky normal form (CNF) in a suboptimal way leading to an avoidable exponential blow-up of the grammar. They neither explain nor discuss whether this can be avoided or not. Complexity analyses often concern the actual CYK procedure only and neglect the pretransformation. Some of the textbooks give vague reasons for choosing CNF, indicating ease of presentation and proof. A few state that CNF is chosen to achieve a cubic running time, not mentioning that only the restriction to binary rules is responsible for that.
We find that this leaves students with wrong impressions. The complexity of solving the word problem for arbitrary CFLs appears to coincide with the complexity of the CYK procedure (ignoring the effects of the grammar transformation). Also, CNF is unduly emphasised.
We believe that this situation calls for correction. We want to show that efficiency and presentability are not contradictory, so that one can teach a less restrictive version of CYK without compromising efficiency of the algorithm, clarity of its presentation, or simplicity of proofs. We propose to use a grammar normal form which is more liberal and easier to achieve than CNF and comes with a linear increase of grammar size only, leading to a faster membership test for arbitrary CFGs.
It would be unnecessary to argue that we should emphasize efficiency concerns as well as ease of presentation in teaching CYK to students, if the goal was just to show that the membership problem for CFLs is decidable. But since CYK is often the only algorithm taught for that problem, students are led to believe that it is also the one which should be used.
Older books on parsing, e.g. Aho and Ullman [1], doubt that CYK "will find practical use" at all, arguing that time and space bounds of O(|w|3) and O(|w|2) are not good enough and that Earley's algorithm does better for many grammars. At least the first part of this may no longer be true. For example, Tomita's [21,19] generalization of LR parsing to arbitrary CFGs uses a complicated "graph-structured" stack to cope with the nondeterminism of the underlying push-down automaton; but Nederhof and Satta [15] show how to obtain an efficient generalized LR parser by using CYK with a grammar describing a binary version of the pushdown automaton. Furthermore, there are non-standard applications of CYK. For instance, Axelsson et al. [3] use a symbolic encoding of CYK for an ambiguity checking test. The claim of Aho and Ullman [1] that CYK is not of practical importance therefore seems too skeptical.
The paper aims at scholars who do know about CYK or, even better, have already taught it. We want to convince them that the standard version can easily be improved and taught so that students learn an efficient algorithm. Note that we only suggest that a particular variant of the algorithm is the best one to teach, not that it should be presented in a particular style.
The paper is organised as follows. Sect. 2 discusses how the CYK algorithm is presented in some prominent textbooks on formal languages, parsing and the theory of computation. Sect. 3 recalls definitions and notations used for languages and CFGs. Sect. 4 presents an efficient test for membership in context-free languages, consisting of the grammar transformation into 2NF, two precomputation steps and the actual CYK procedure. Correctness proofs and complexity estimations are given for each of the steps. The section finishes with an example.1 Sect. 5 contains some concluding remarks about teaching the variant proposed here and the possibility of avoiding grammar transformations at all.
2 The CYK Algorithm in Textbooks
What is understood as the CYK algorithm? For textbooks on formal languages, the input of the CYK algorithm is a context-free grammar G in Chomsky normal form (CNF) and a word w over the terminal alphabet of G; its output is a recognition table T containing, for each subword v of w, the set of nonterminals that derive v, i.e. its syntactic properties. In particular, T tells us whether w is a sentence of G. Thus, the membership problem for G is solved, and by transforming an arbitrary context-free grammar into an equivalent one in CNF, the membership problem for context-free grammars is solved as well.
Using some standard notation explained below, figure 1 shows a typical version of CYK, where the nonterminals deriving the subword ai...aj of w are stored in Ti,j.
| input: a CFG G = (N,Σ,S,→) in CNF, a word w = a1...an ∈ Σ+ |
| CYK(G,w) = |
| 1 for i=1,...,n do |
| 2 Ti,i : = {A ∈ N | A→ ai} |
| 3 for j=2,...,n do |
| 4 for i=j-1,...,1 do |
| 5 Ti,j : = ∅; |
| 6 for h=i,...,j-1 do |
| 7 for all A → BC |
| 8 if B ∈ Ti,h and C ∈ Th+1,j then |
| 9 Ti,j : = Ti,j ∪{ A } |
| 10 if S ∈ T1,n then return yes else return no |
Figure 1: Algorithm CYK for the word problem of CFGs in CNF.
Concerning the restriction to CNF, a little reflection shows that the basic idea of CYK can be extended to arbitrary context-free grammars (and beyond [11,16]). The syntactic properties of w can be computed from the syntactic properties of all strict subwords v of w using a dynamic programming approach: store the nonterminals deriving v in table fields Tv and compute Tw by combining entries in stored Tv's according to rules of G and all possible splittings of w into at most m strict subwords v, where m is the maximum number of symbols in the right hand sides of grammar rules. This gives an algorithm solving the word problem for context-free grammars in time O(|w|m+1).
Such a remark is generally absent in textbooks on formal languages. Among the computer science books on parsing, only Aho and Ullman [1] remark that "a simple generalization works for non-CNF grammars as well"; among those in computational linguistics one can find a generalization of the CYK algorithm to acyclic CFGs without deletion rules in Winograd's book [23], c.f. Naumann and Langer [13]. The latter then motivates the restriction to CNF by a "simplification to compute T", without going into any detail. Aho and Ullman [1] say that CNF "is useful in simplifying the notation needed to represent a context-free language". Textbooks on formal languages motivate the restriction to CNF by the fact that "many proofs can be simplified" if right-hand sides of rules have length at most two [7], or claim that the advantage of CNF "is that it enables a simple polynomial algorithm for deciding whether a string can be generated by the grammar" [12]; this is only correct if the emphasis lies on "simple". In fact, there is a mixture of two reasons for using grammars in CNF in CYK: cutting down the time complexity to O(|w|3) and keeping the correctness and completeness proofs simple. The textbooks on formal languages do not clearly say which of the restictions of the CNF format serves which of these goals.
In the literature on parsing, one can find a number of variations of CYK that differ in the restrictions on the input grammar. The most liberal one that suffices to make CYK run in time O(|w|3) is that the grammar is bilinear, i.e. in each rule A→α there are at most two nonterminal occurrences in α, see the so-called C-parser [10]. Others relax the CNF restriction by admitting unit rules, i.e. rules A→ α where α is a nonterminal [20]. Almost all textbooks on formal languages stick to the very restrictive CNF, where in each rule A→α either α = BC for nonterminals B and C, or α is a terminal, or α is the empty word ε and A is the start symbol and must not be used recursively. Then any context-free language has a grammar in CNF. For some variations of the definition, obviously motivated by simplicity of presentation, this only holds for languages without words of length 0 or 1. Given this variety, we draw the conclusion that CYK is to be understood as the above sketched algorithm that uses dynamic programming and context-free grammars in some normal form to solve the membership problem in time O(|w|3).
|
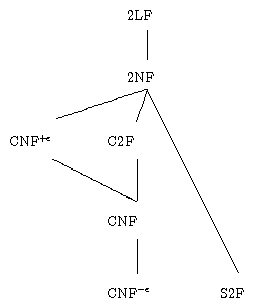 |
Chomsky normal form (CNF), strict 2-form (S2F),
canonical 2-form (C2F), 2-normal form (2NF), bilinear form (2LF)
Table 1: Grammar normal forms and their hierarchy w.r.t. inclusion
Table 1 defines the normal forms that are being used in textbooks (apart from our proposal 2NF) and shows how they relate to each other. In the column "rule format", A,B,C are arbitrary nonterminals, S is the start symbol that may not occur on a right-hand side, a is a terminal symbol, u,v,w are strings of terminal symbols, and α is a sentential form.
Table 2 lists, for several books that present a version of CYK, the format of the normal form they require and the asymptotic time and space complexity they state for their CYK procedure on grammars in the respective normal form. One can see that the most prominent textbooks on formal language theory ignore the dependency on the grammar. Furthermore, they demand a very restrictive normal form compared to other books which obtain reasonable complexity bounds.
| Book | Subject | Format | Time | Space |
| Aho/Ullman '72 | Pa | CNF | |w|3 | - |
| Hopcroft/Motwani/Ullman '01 | CT | CNF-ε | |w|3 | - |
| Harrison '78 | FL | CNF | |w|3 | |w|2 |
| Naumann/Langer '94 | Pa | CNF-ε | |w|3 | |w|2 |
| Schöning '00 | CT | CNF-ε | |w|3 | - |
| Sippu/Soisalon-Soininen '88 | Pa | C2F | |G|·|w|3 | |N|·|w|2 |
| Wegener '93 | CT | CNF-ε | |G|·|w|3 | - |
| Lewis/Papadimitriou '98 | CT | S2F | |G|·|w|3 | |N|·|w|2 |
| Rich '07 | CT | CNF-ε | |G| ·|w|3 | - |
| Autebert/Berstel/Boasson '97 | FL | CNF+ε | - | - |
Subject: parsing (Pa), formal languages (FL), theory of computation (CT)
G is the input grammar, N its nonterminal set, and w is the input word.
Table 2: Overview over variants of CYK, with complexity mentioned
Transforming CFGs into CNF Most textbook solutions to the word problem for context-free grammars present the CYK algorithm for grammars in CNF and just state that this is no restriction of the general case. A complexity analysis is often done only for the CYK procedure. Where a complexity analysis for the transformation into CNF is missing, one obtains the impression that the membership problem for CFGs can be solved within the same bounds as for grammars in CNF. This is true but almost never achieved with the procedure presented in these textbooks. Consequently, most students will not be able to tell whether an algorithm like CYK is possible for arbitrary CFGs, and almost none will know the time complexity of the membership problem for arbitrary CFGs in terms of grammar size. This is problematic not only for computational linguistics, where the grammar size is huge compared to sentence length.
The transformation to CNF combines several steps: the eliminiation of terminal symbols except in right hand sides of size 1 (TERM); the reduction to rules with right-hand sides of size ≤ 2 (BIN); the elimination of deletion rules (DEL); and the elimination of unit rules (UNIT). It is often neglected that the complexity of the transformation to CNF depends on the order in which these steps are preformed.
- The blow-up in grammar size depends on the order between DEL and BIN. It may be exponential when DEL is done first, but is linear otherwise.
- UNIT can incur a quadratic blow-up in the size of the grammar.
Hence, except for TERM, which gives a linear increase in grammar size, the order in which the single transformation steps are carried out should be: BIN → DEL → UNIT. This will yield a grammar of size O(|G|2). Nevertheless, many textbooks choose a different order, namely DEL → UNIT → BIN which yields a grammar of size O(22|G|). Even worse so, only few textbooks contain a rigorous complexity analysis of this transformation or a hint at its suboptimality.
Table 3 shows how the textbooks mentioned in Table 2 handle the transformation into the normal form that their CYK variant demands, i.e. the one listed in column "rule format" of Table 2. The last two columns give the asymptotic size of the resulting grammar and the fact whether or not the estimation is given in the textbook. Table 4 shows the asymptotic time complexity for the word problem that one obtains by combining their transformation to normal form with their corresponding version of CYK.
| Book | Target | Method | |G'| | Stated |
| Aho e.a. | CNF | DEL → UNIT → BIN → TERM | 22|G| | - |
| Hopcroft e.a. | CNF-ε | DEL → UNIT → TERM → BIN | 22|G| | - |
| Harrison | CNF | DEL → UNIT → TERM → BIN | 22|G| | - |
| Naumann e.a. | (refers to Aho e.a.) | |||
| Schöning | CNF-ε | DEL → UNIT → TERM → BIN | 22|G| | - |
| Sippu e.a. | C2F | BIN → DEL | |G| | + |
| Wegener | CNF-ε | TERM → BIN → DEL → UNIT | |G|2 | + |
| Lewis e.a. | S2F | BIN → DEL → UNIT | |G|3 | + |
| Rich | CNF-ε | BIN → DEL → UNIT → TERM | |G|2 | + |
| Autebert e.a. | CNF+ε | TERM → BIN → UNIT | |G|2 | - |
| This paper | 2NF | BIN | |G| | + |
Wegener [22] gives O(|V|·|G|) as |G'|, but ignores that BIN increased V to size |G|.
Table 3: Transformation of CFG (with only useful symbols) into NF
Which normal form to choose? All normal forms mentioned in Table 1 allow for a time complexity of CYK that is cubic in the size of the input word and linear in the size of the grammar. Therefore, the question which of the possible normal forms to choose ought to be determined by two factors: (i) complexity of the grammar transformation, in particular the size of the transformed grammar, and (ii) ease of presentation and proofs.
To simplify the discussion, we only consider grammars for e-free languages, on which CNF and CNF-εcollapse. Simplicity of the grammar transformation and size of the resulting grammar would suggest to favour 2NF over C2F or CNF. The transformation to 2NF only needs step BIN with a linear increase in grammar size. The transformation to C2F needs the additional step DEL, but is also linear, provided that BIN is executed before DEL. Transformation to CNF affords the additional steps of UNIT and TERM. Step UNIT causes a quadratic inrease in grammar size and therefore ought to be omitted. TERM can be achieved by a linear blow-up of the grammar, but has no real advantage for the complexity or presentation of CYK, so we prefer to omit it. Although 2LF is more liberal than 2NF, the latter is preferable since the transformation to 2NF is simpler to explain.
But what is the price to pay in terms of modifications of CYK or the proofs involved? Unit rules and deletion rules in the grammar seem to complicate the filling of the recognition table: in order to compute Tv, one now has to consider splittings v=v1v2 not only into strict subwords v1,v2, but also non-strict ones, say v1=e, v2=v. Actually, a small modification of the original version of CYK suffices to accommodate for deletion and unit rules: just close the fields Tv under the rule "if B ∈ Tv and A⇒*B, add A to Tv". This can be done efficiently, as shown by Sippu and Soisalon-Soininen [20] or below.
However, this is part of what is done in transformations to CNF as well: in order to eliminate deletion rules from a grammar, one computes the set of nullable nonterminals, and in order to eliminate unit rules, one computes the set of nonterminals that derive a given one [1,7,8]. But, rather than using these relations to transform the grammar to CNF, one can use them in the CYK algorithm directly and leave the (2NF) grammar unchanged. We think the explicit use of auxiliary information is better than an unnecessary transformation of input data.
In our opinion, the advantage of using 2NF or C2F over CNF in CYK is not reflected well in the literature. We are only aware of one textbook which presents the CYK algorithm for grammars in C2F, [20] - a specialised book on parsing - and a PhD thesis [14]. It seems to have been unnoticed so far that one can use even 2NF instead of C2F. We consider 2NF as an advantage over C2F, since not only unit rules, but also deletion rules are convenient in grammar writing; the latter are often used as a means to admit optional constituents. Furthermore, as we will show below, using 2NF does not compromise on the ease of presentation nor proof.
| Book | via | Time | Stated |
| Aho e.a. | CNF | 22|G| ·n3 | - |
| Hopcroft e.a. | CNF-ε | 22|G| ·n3 | - |
| Harrison | CNF | 22|G| ·n3 | - |
| Naumann e.a. | CNF | 22|G| ·n3 | - |
| Schöning | CNF-ε | 22|G| ·n3 | - |
| Sippu e.a. | C2F | |G|·n3 | + |
| Wegener | CNF-ε | |G|2 ·n3 | + |
| Lewis e.a. | S2F | |G|3 ·n3 | + |
| Rich | CNF-ε | |G|2 ·n3 | + |
| Autebert e.a. | CNF+ε | |G|2 ·n3 | - |
| This paper | 2NF | |G|·n3 | + |
The last column states whether or not the overall time complexity is given.
Table 4: Upper complexity bounds for the word problem on arbitrary CFGs
3 Preliminaries
Let Σ be a finite set, called the alphabet. A letter is an element of Σ, a word is a finite sequence of letters, and a language is a set of words. Σ* is the set of all words over Σ, and Σ+ the set of all nonempty words. As usual, ε is used for the empty word, wv for the concatenation of the two words w and v, and |w| for the length of the word w, with |ε| = 0. For a word w = a1...an and positions 1 ≤ i ≤ j ≤ n we write w[i..j] for the subword ai...aj of w.
A context-free grammar (CFG) is a tuple G = (N,Σ,S,→) s.t.
- Σ is the finite alphabet or set of terminals;
- N is the finite non-empty set of nonterminals, s.t. N ∩Σ = ∅;
- S ∈ N is the start symbol;
- → ⊆ N ×(N ∪Σ)* is a finite set of rules.
The set of all symbols of G is N ∪Σ, which will always be denoted by the letter V in the following. We will use uppercase letters like A,B,C to denote nonterminals, lowercase letters like a,b,c to denote terminal symbols, small letters like x,y,z to denote symbols, lowercase letters like u,v,w to denote words over Σ, and Greek lowercase letters α,β,γ,... for sentential forms, i.e. words over V. Henceforth we simply use grammar for context-free grammar.
A grammar can be represented by enlisting, for each nonterminal A, the right-hand sides α of rules A → α. Thus, one measures the size of G by
| |G| : = | ∑ A ∈ N |
∑ A → α |
|Aα|. |
We assume that each symbol occurs in some rule, so that |V| ∈ O(|G|).
The derivation relation ⇒ ⊆ V+×V* is defined such that for all α,β ∈ V*, αA β⇒ αγβ iff there is a rule A → γ. The relations ⇒n, ⇒+ and ⇒* are the n-fold iteration, the transitive closure, and the reflexive-transitive closure of ⇒, respectively.
The language generated by G is L(G) : = { w ∈ Σ* | S ⇒+ w }. Two context-free grammars G1,G2 with the same terminal alphabet are equivalent if L(G1)=L(G2).
Definition 1 A grammar G = (N,Σ,S,→) is in binary normal form (2NF) if for all A →α we have |α| ≤ 2.
In our exposition of the CYK algorithm, a predicate on nonterminals and a relation between symbols of a grammar play an important role.
Definition 2 The set of nullable symbols of the grammar G = (N,Σ,S,→) is
|
and the unit relation of G is
| UG : = { (A,y) | ∃α,β ∈ EG* with A → αy β}. |
4 The Word Problem for Context-Free Languages
We suggest the following algorithm to test, for a given grammar G and a given word w, whether or not w ∈ L(G).
- Preprocessing of the grammar.
- Transformation of G into an equivalent G' in 2NF.
- Computation of the set EG' of nullable symbols in G'.
- Construction of the inverse unit relation ÛG' of G'.
- Building the CYK table for w and (G',ÛG').
4.1 Transformation into 2NF
It is well-known that every grammar can be transformed into an equivalent one in CNF, applying the four transformations TERM, BIN, DEL, UNIT mentioned in the introduction. Every grammar can be transformed into one in 2NF by just performing the step BIN.
Lemma 1 For every grammar G = (N,Σ,S,→) there is an equivalent grammar G' = (N',Σ,S,→') in 2NF computable in time O(|G|), such that |G'| = O(|G|), |N'| = O(|G|).
Proof The transformation BIN replaces each rule A→ x1x2...xn with n > 2 by the rules A →' x1〈x2,...,xn〉, 〈x2,...,xn〉 →' x2 〈x3,...,xn〉, ..., 〈xn-1,xn〉 →' xn-1xn, abbreviating suffixes of length ≥ 2 by new symbols 〈xi,...,xn〉 ∈ N'. This can be carried out in a single pass through the grammar, and the number of new nonterminals is bounded by the size of G. The equivalence of G' and G can easily be shown by transforming derivations with G' into derivations with G and vice versa.
In fact, G' is a left-cover of G: any leftmost derivation with respect to G' is mapped to a leftmost derivation with respect to G by replacing applications of A→'x1〈x2,...,xn〉 with applications of A→ x1 x2...xn and omitting applications of 〈xi,...,xn〉 →' xi〈xi+1,...,xn〉 and 〈xn-1,xn〉 →' xn-1xn.
 |
→ |  |
4.2 Precomputation of the Nullable Symbols
The following lemma gives an inductive characterisation of EG.
Lemma 2 Let G = (N,Σ,S,→) be a grammar. Then EG = E|N| where
|
Proof (" ⊇ ") By induction on i, one shows Ei ⊆ EG for all i.
(" ⊆ ") By definition, Ei ⊆ Ei+1 ⊆ N for any i. As N is finite, E|N|+1 = E|N|. To show EG ⊆ E|N|, prove by induction on n that A⇒n ε implies A ∈ E|N|.
Lemma 2 suggests to construct EG by iteratively computing the Ei until Ei+1=Ei. A naïve implementation of this idea can easily result in quadratic running time. However, it is possible to compute EG in time linear in the grammar, as mentioned by Harrison [7], Exercise 2 in Section 4.3, and Sippu e.a. [20], Theorem 4.14. Since this seems not to be well-known, we present in Fig. 2 an algorithm Nullable to do so for G in 2NF. It maintains a set todo which can be implemented as a list with insertion of an element and removal of the first one in constant time, and a set nullable which should be stored as a boolean array with constant access time.
Algorithm Nullable successively finds those nonterminals that can derive ε starting with those that derive it in one step and proceeding backwards through the rules. For this, the predecessors of a nonterminal B, i.e. all the nonterminals A such that B occurs on the right-hand side of a rule A → α, need to be accessible without searching through the entire grammar. The algorithm therefore starts by storing in an initially empty array occurs the set of all such A for each such B. This information is used to infer from the information that B is nullable, that A is also nullable, if A and B are linked through a rule A→ B. If they are linked through a rule A →BC or A → CB then this depends on whether or not C is nullable too. Hence, the array occurs actually holds for a rule of the form A → B the nonterminal A, and for a rule of the form A → BC or A → CB, the pair 〈A,C〉. This is then used in order to avoid quadratic running time.
| input: a CFG G = (N,Σ,S,→) in 2NF |
| Nullable(G) = |
| 1 nullable : = ∅ |
| 2 todo : = ∅ |
| 3 for all A ∈ N do |
| 4 occurs(A) : = ∅ |
| 5 for all A → B do |
| 6 occurs(B) := occurs(B) ∪{ A } |
| 7 for all A → BC do |
| 8 occurs(B) := occurs(B) ∪{ 〈A,C〉} |
| 9 occurs(C) := occurs(C) ∪{ 〈A,B 〉} |
| 10 for all A → e do |
| 11 nullable : = nullable ∪{A} |
| 12 todo : = todo ∪{A} |
| 13 while todo ≠ ∅ do |
| 14 remove some B from todo |
| 15 for all A, 〈A,C〉 ∈ occurs(B) with C ∈ nullable do |
| 16 if A ∉ nullable then |
| 17 nullable : = nullable ∪{A} |
| 18 todo : = todo ∪{A} |
| 19 return nullable |
Figure 2: Algorithm Nullable for the linear-time computation of EG.
Lemma 3 For any grammar G = (N,Σ,S,→) in 2NF, algorithm Nullable computes EG in time and space O(|G|).
Proof Clearly, the four for-loop in lines 3-12 can be executed in time O(|N|), resp. O(|G|). For the while-loop note that no nonterminal B can be inserted into todo once it has been removed from it, because then it is on nullable. Hence, the while-loop can be executed at most |N| times. For each nonterminal B, the inner for-loop is executed a number of times that is given by the number of occurrences of B in the right-hand side of a rule. Since G is assumed to be in 2NF, the combined number of iterations between the outer while- and the inner for-loop is bounded by 2·|G|. Furthermore, all the other instructions can be executed in constant time yielding an overall running time of O(|G|).
The space needed is O(|N|) for the sets todo and nullable and O(|G|) for the array occurs. Hence, it is bounded by O(|G|).
4.3 Constructing the Unit Relation
As a consequence of Lemma 3, we can also compute the unit relation efficiently:
Lemma 4 Let G be a grammar in 2NF. The unit relation UG and its inverse,
|
can be computed in time and space O(|G|).
We view ÛG as a relation on V and call IG = (V,ÛG) the inverse unit graph of G.
Proof According to Lemma 3, EG can be computed in time and space O(|G|). To construct IG in linear time and space, first add a node for every symbol in V. Then, for every rule A → y, A → By and A → yB with B ∈ EG, add the edge (y,A) to ÛG.
This gives us ÛG as a list of length O(|G|), generally with multiple entries. We can similarly output a list of length |V| of nodes y associated with a list of their UG-predecessors A1,...,An, i.e. a representation of the graph IG as needed in Lemma 6 below. (We could, but need not remove duplicates in the given time and space bound.)
Algorithm CYK below will need, for a given set M of symbols, the set of all x such that there is a y ∈ M and x ⇒* y. We show that the restriction of ⇒* to V×V is the reflexive-transitive closure UG* of the unit relation of G.
Lemma 5 Let G = (N,Σ,S,→) be a grammar. Then for all x,y ∈ V we have: x ⇒* y iff (x,y) ∈ UG*.
Proof ("only if") Suppose x ⇒* y, i.e. there is an n ∈ N with x ⇒n y. If n = 0, then (x,y) ∈ UG* because UG* is reflexive. If n > 0, there is x→γ with γ⇒n-1 y. Since y is a single symbol, γ = αzβ for suitable α,β,z such that z ∈ V, z ⇒n1 y and αβ⇒n2 ε for some n1,n2 with 1 ≤ n1 + n2 < n. By induction hypothesis we have (z,y) ∈ UG*, and by Lemma 2, αβ ∈ EG*. But then (x,z) ∈ UG ⊆ UG*, and since UG* is transitive, (x,y) ∈ UG*.
("if") Since UG* is the (w.r.t. ⊆ ) least reflexive and transitive relation that subsumes UG, we only need to show that ⇒* subsumes UG. But when (x,y) ∈ UG, there are α,β ∈ EG* such that x→ αyβ, and then x ⇒* y since αβ⇒*ε.
It follows that for any M ⊆ V, the set of all x ∈ V which derive some element of M, is just {x | ∃y ∈ M, (x,y) ∈ UG*} and hence equals
|
To compute such sets efficiently, we do not build the relation ÛG*, which can be quadratic in the size of ÛG and G, but use the inverse unit graph:
Lemma 6 Let G be a grammar in 2NF with symbol set V. Given its inverse unit graph IG, the set ÛG*(M) can be computed in time and space O(|G|), for any M ⊆ V.
Proof ÛG*(M) consists of all nodes x ∈ V that are reachable in IG from some node y ∈ M. The set of all nodes in a graph reachable from a given set of nodes can be computed in time and space O(n + m) where n is the number of all nodes and m the number of all edges. This simply uses depth- or breadth-first search [5]. Hence, ÛG*(M) can be computed in time and space O(|V| + |UG|) = O(|G|).
Clearly, one could drop the assumption that IG be given, as it can be constructed from G in time and space O(|G|). However, since we will need to compute ÛG*(M) for several M, it is advisable to construct IG once and for all at the beginning only.
4.4 Building the CYK Table
The membership problem for a context-free grammar G=(N,Σ,S,→), i.e. to determine for words w ∈ Σ* whether S⇒+ w or not, generalizes naturally to the computation of the sets { x | x ∈ V, x ⇒* v } of all symbols of G that derive v, for all subwords v of w. These sets can be constructed inductively.Theorem 7 Let G = (N,Σ,S,→) be a grammar in 2NF, (V,ÛG) its inverse unit graph, and w ∈ Σ+. Then for any x ∈ V and any non-empty subword v of w we have x ⇒* v iff x ∈ Tv, where the sets Tv and the auxiliary sets T'v are defined by
|
Proof ("if") We prove this by induction on |v|. Suppose x ∈ Tv. Then there is a y ∈ T'v s.t. (x,y) ∈ UG*, and by Lemma 5, x⇒*y.
Suppose |v| = 1. By the definition of T'v we have y = v which immediately yields x ⇒* v.
Now suppose |v| ≥ 2. Then y ∈ T'v is only possible if there is a splitting v=v1v2 of v into two non-empty subwords and a rule x→ z1z2 such that z1 ∈ Tv1 and z2 ∈ Tv2. Hence, the hypothesis yields z1 ⇒* v1 and z2 ⇒* v2. But then we have x ⇒* y ⇒ z1z2 ⇒* v1z2 ⇒* v1 v2 = v.
("only if") Suppose x ⇒* v. There is n ≥ 0 such that x⇒n v. By induction on n, we show that x ∈ Tv. The base case of n=0 means x=v, and in particular |v| = 1 since x ∈ V. But then x ∈ T'v and, hence, x ∈ Tv.
Now suppose that n > 0. Since G is 2NF and v ≠ ε, the first rule applied in the derivation is of the form (i) x→ y with y ∈ V, or (ii) x→ y1 y2 with y1,y2 ∈ V. In case (i), we have y ⇒n-1 v, and hence y ∈ Tv by hypothesis. Since Tv is closed under the inverse of UG, we also have x ∈ Tv.
In case (ii), the derivation is of the form x ⇒ y1y2 ⇒n-1 v. Then there is a splitting v=v1v2 of v such that y1⇒m1v1 and y2⇒m2v2 with m1,m2 < n. If v1 = ε then v2 ≠ ε and we have y2 ∈ Tv2 by the hypothesis, and x ⇒ y1y2 ⇒* y2. Hence, by Lemma 5, (x,y2) ∈ UG* and, since Tv2 is closed under the inverse of UG*, also x ∈ Tv2 = Tv. Equally, if v2 = ε then v1 ≠ ε and y1 ∈ Tv1 by hypothesis, which also yields x ∈ Tv1 = Tv. If v1,v2 both differ from ε, we get y1 ∈ Tv1 and y2 ∈ Tv2 both from the hypothesis and therefore x ∈ T'v which entails x ∈ Tv.
Algorithm CYK in Fig. 3 contains an implementation of the procedure that is implicitly given in Thm. 7. It computes, on a G in 2NF and a word w=a1...an of length n, for each 1 ≤ i ≤ j ≤ n the set Tai...aj of Theorem 7, which is here called Ti,j.2 These are stored in an array of size n2, with a boolean array of size |N| as entries, plus a terminal in the fields on the main diagonal. Initially, all fields in the boolean arrays are set to false. Algorithm CYK assumes the inverse unit graph IG to have been computed already.
Note that algorithm CYK only differs minimally from most textbook versions of CYK, e.g. [8,7]: these do not close the table entries under ÛG* as done here in lines 2 and 10. Also note that CYK presupposes the input word w to be non-empty. The case of the input ε can - as with all other CYK versions - easily be dealt with separately since EG needs to be computed anyway and ε ∈ L(G) iff S ∈ EG.
| input: | a CFG G = (N,Σ,S,→) in 2NF, its graph (V,ÛG),a word w = a1...an ∈ Σ+ |
| CYK(G,ÛG,w) = | |
| 1 for i=1,...,n do | |
| 2 Ti,i : = Û*G({ai}) | |
| 3 for j=2,...,n do | |
| 4 for i=j-1,...,1 do | |
| 5 T' i,j : = ∅ | |
| 6 for h=i,...,j-1 do | |
| 7 for all A → yz | |
| 8 if y ∈ Ti,h and z ∈ Th+1,j then | |
| 9 T' i,j : = T' i,j ∪{ A } | |
| 10 Ti,j : = Û*G(T' i,j) | |
| 11 if S ∈ T1,n then return yes else return no |
Figure 3: Algorithm CYK for the word problem of CFG in 2NF.
Lemma 8 Given a grammar G = (N,Σ,S,→) in 2NF, its graph IG and a word w ∈ Σ+, Algorithm CYK decides in time O(|G|·|w|3) and space O(|G|·|w|2) whether or not w ∈ L(G).
Proof The for-loop in lines 1-2 takes time O(|w|·|G|). The inner loop in lines 7-9 is executed O(|w|3) times, each iteration taking O(|G|) steps, and each step being executed in constant time. Line 10 is executed O(|w|2) times, taking O(|G|) steps for each execution according to Lemma ) steps for each execution according to Lemma 6. This amounts to O(|w|·|G| + |G|·|w|3 + |G|·|w|2) = O(|G|·|w|3) altogether.
The space needed to store T is O(|w|2 ·|N|) and the one to compute ÛG*(Ti,j) is O(|G|). Hence, we need space O(max{|w|2·|N|,|G|}) ≤ O(|w|2·|G|) altogether.
Lemma 8 expects G to be in 2NF and IG given already. Solving the word problem for arbitrary context-free grammars requires the transformation and precomputation to be done beforehand.
Corollary 9 The word problem for context-free grammars G and words of length n can be solved in time O(|G| ·n3) and space O(|G|·n2).
Proof First, transform G into an equivalent G' in 2NF with |G'| = O(|G|). By Lemma ). By Lemma 1, this can be done in time and space O(|G|) . Then, compute the set of nullable nonterminals and the inverse unit graph for G' in time and space O(|G'|) according to Lemma ) according to Lemma 2 and Lemma 4. Finally, execute CYK in time O(|G'| ·n3) and space O(|G'|·n2) according to Lemma 8.
Since |G'| is O(|G|), this yields an asymptotic running time of O(|G| · n3) and a space consumption of O(|G| ·n2).
4.5 An Example
We finish this section by executing the entire procedure on the following example grammar G over the alphabet Σ = {a,b,0,1,(,),+,*}.
| E | → | T | E + T |
| T | → | F | T * F |
| F | → | aI | bI | (E) |
| I | → | 0I | 1I | ε |
First we need to transform G into 2NF by introducing new nonterminals X, Y, Z for the right-hand sides that are larger than 2 symbols. The result is the following grammar G' with symbol set V.
|
It has 7 nonterminals, 13 rules, and is of size 35. Since most textbook versions of CYK would require G to have been transformed into CNF, we state the corresponding figures for the resulting CNF grammar without presenting it explicitly. If it is obtained in the order DEL → UNIT → TERM → BIN, then the result has 15 nonterminals, 33 rules, and is of size 83.
It is easy to see that only I is nullable, i.e. EG' = { I }. In order to be able to compute ÛG*(M) for any M ⊆ V we first determine the unit relation.
|
Hence, we have, for instance
|
etc.
| j=1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
( |
E,T F |
E T |
i=1 | |||||
| E,T,F a |
E,T F |
E |
Z |
2 | ||||
| I 0 |
3 | |||||||
+ |
X |
4 | ||||||
| E,T,F b |
Z |
5 | ||||||
) |
6 | |||||||
* |
Y |
7 | ||||||
| E,T,F a |
8 |
To finish the example, consider the word w = (a0 + b) * a. Executing CYK on w creates the table depicted in Fig. 4. It is to be understood as follows. A nonterminal A in the bottom half of an entry at row i and column j belongs to T'v for v=w[i..j]. Hence, it is in there because of a rule of the form A → yz such that y and z occur at certain positions in the same row to the left and in the same column below. A nonterminal in the top half of the entry belongs to Tv\T'v, i.e. it is in there because it is a predecessor in ÛG* of some nonterminal from the bottom half. Hence, the entire entry represents Tv. The bottom halves of the entries on the main diagonal always form the input word when read from top-left to bottom-right.
4.6 Parsing with CYK
The CYK recognition algorithm can be turned into a parser either by constructing parse trees from the recognition table or by inserting trees rather than nonterminals into the table. We only discuss how to construct parse trees from the table, leaving aside the question of space-efficient structure sharing for a table holding trees.
In the case of CYK for grammars in CNF, define a function extract(A,i,j) that returns for A ∈ Ti,j the trees with root labelled A and yield ai...aj by
|
where A(s,t) is the tree with root labelled A and immediate subtrees s and t. Since grammars in CNF are acyclic (i.e. A⇒+A does not occur), the number of parse trees of a given w is finite, and all possible parse trees can be obtained from the table in finitely many steps.
Our CYK uses grammars in 2NF, which may be cyclic and hence may have inputs with infinitely many parses. We adapt the tree extraction algorithm so that it returns a finite number of "essentially different" analyses. First, for x ∈ Ti,j' an auxiliary function extract'(x,i,j) returns trees with yield ai...aj and root labelled x, which are leaves in case i=j or branch at the root to two subtrees, each having a nonempty yield. Then, for A ∈ Ti,j, extract(A,i,j) extends such trees by adding a root labelled A on top, if A⇒+x:
|
Using extract, we consider all derivations A⇒+x as inessential variants of each other and represent them as a unary branch. Since these branches generally do not correspond to grammar rules A→ x, the extracted trees are not parse trees in the strict sense. If the grammar is acyclic, we can turn them into parse trees: in this case, for each (A,x) ∈ UG+, there are only finitely many derivations A⇒+x, so their parse trees can be precomputed and extract(A,i,j) would put them on top of the trees returned by extract'(x,i,j). If the grammar is cyclic, we can still precompute the finite number of derivations A⇒+x which have no subderivations B⇒+B, and by using them in extract(A,i,j), we would obtain a finite set of "canonical" parse trees. In this way, we get a correct but incomplete parser. (Note that the missing parse trees with subderivations B⇒+B also get lost if we turn the grammar into CNF.)
Suppose CYK is used with a 2NF grammar G' for a given grammar G and a word w. Since G' is a left-cover of G by Lemma is a left-cover of G by Lemma 1, it is easy to recover w's parse trees with respect to G from those for G' obtained by CYK. One just has to undo the transformation of k-ary branching rules to binary branching ones on the trees, i.e. apply the covering homomorphism on left parses. In this way, the finitely many "canonical" parse trees with respect to G' can be transformed into parse trees with respect to G. If G' is acyclic, this gives a complete parser for G.
5 Conclusion
Teaching CYK with pretransformation into 2NF The variant of CYK we propose here is not more difficult to present than those in the standard textbooks. The precomputations that this CYK version requires need to be done in the textbook versions as well where they are part of the grammar transformation: the computation of the nullable symbols is necessary for step DEL; the construction of the inverse unit graph could also be used to implement step UNIT. We believe that using these relations explicitly in the CYK algorithm is better from a learning point of view than to use them in order to transform the grammar. By using them in the algorithm one cannot do the BIN- and DEL-transformations in the wrong order and automatically avoids an exponential blowup of the grammar. Moreover, it emphasises the fact that the computation of such relations is a necessary means to solving the membership problem, and it will therefore make it easier for students to remember it.
On the other hand, one may argue that the essence of CYK is the dynamic programming technique and that therefore the actual algorithm should not contain computation steps which obfuscate the view onto that technique. However, our algorithm CYK only differs in two lines (the closure steps in lines 2 and 9) from those that work on CNF input.
As shown in the introduction, many textbooks ignore the complexity of the normal form transformation or ignore the dependency of CYK's complexity on the size of the input grammar. We believe that this is wrong in cases where the blow-up in the grammar is suboptimal. It is obviously possible to present our variant of CYK without the complexity analyses. If this is done, then using the 2NF variant bears two distinct advantages over the CNF variant: (1) It does not contain hidden obstacles like the dependency of the blow-up on the order in which the pretransformation steps are done. (2) Since the CNF transformation comes with an at least quadratic blow-up in grammar size, one may be inclined to think that the complexity of the word problem for arbitrary CFGs is at least quadratic in the grammar size. The 2NF variant does not give this impression.
Finally, note that in the previous two sections we have presented one way of presenting this variant of CYK. The essentials are easily seen to be the 2NF transformation, the computation of the nullable symbols, the linear time and space algorithm for computing the predecessors w.r.t. ⇒*, and algorithm CYK. The correctness proofs are of course not essential in order to obtain an efficient procedure. They can be left out, as is done in many textbooks.
A tool is available that is meant to support teaching this variant of CYK3. It visualises the entire procedure presented here on arbitrary input context-free grammars. In particular, it shows simulations of the computation of the nullable symbols, the inverse chain relation, and the filling of the CYK table.
Avoiding normal forms at all We have argued for omitting the grammar transformation steps TERM, UNIT and DEL in favour of precomputed auxiliary relations. One may push this a step further and teach a version of CYK which omits the transformation BIN as well and only implicitly works with binary branching rules. To do so, one would not only insert symbols x ∈ V into the fields Tv of the recognition table, but also "dotted rules" A→α·β where A→αβ is a grammar rule and α⇒* v. The algorithm would have to close the table under the rules
|
where the field identifiers are subwords of the input sentence and ·ε = ε·. However, this would be a step away form the simplicity of CYK towards Earley's algorithm [·. However, this would be a step away form the simplicity of CYK towards Earley's algorithm [6], and seems less memorizable than the explicit transformation to 2NF. We therefore conclude that the pretransformation into 2NF and the according variant of CYK forms the best balance between didactic needs and the aim for efficiency.
References
- [1]
- A. V. Aho and J. D. Ullman. The Theory of Parsing, Translation, and Compiling, volume Volume I: Parsing. Prentice-Hall, 1972.
- [2]
- J. Autebert, J. Berstel, and L. Boasson. Context-free languages and pushdown automata. In A. Salomaa and G. Rozenberg, editors, Handbook of Formal Languages, volume 1, Word Language Grammar, pages 111-174. Springer-Verlag, Berlin, 1997.
- [3]
- R. Axelsson, K. Heljanko, and M. Lange. Analyzing context-free grammars using an incremental SAT solver. In Proc. 35th Int. Coll. on Automata, Languages and Programming, ICALP'08, Part II, volume 5126 of LNCS, pages 410-422. Springer, 2007.
- [4]
- J. Cocke and J. T. Schwartz. Programming Languages and Their Compilers. Courant Institute of Mathematical Sciences, New York, 1970.
- [5]
- T. H. Cormen, C. E. Leiserson, and R. L. Rivest. Introduction to Algorithms. MIT Press, McGraw-Hill, Cambridge, London, 1990.
- [6]
- Jay Earley. An efficient context-free parsing algorithm. Communications of the ACM, 13(2):94-102, 1970.
- [7]
- M. A. Harrison. Introduction to Formal Language Theory. Addison-Wesley series in computer science. Reading (MA): Addison-Wesley, 1978.
- [8]
- J. E. Hopcroft, R. Motwani, and J. D. Ullman. Introduction to Automata Theory, Languages, and Computation. Addison-Wesley, New York, 3 edition, 2001.
- [9]
- T. Kasami. An efficient recognition and syntax analysis algorithm for context-free languages. Technical Report AFCRL-65-758, Air Force Cambridge Research Laboratory, Bedford, Massachusetts, 1965.
- [10]
- R. Leermakers. How to cover a grammar. In 27th Annual Meeting of the ACL, Proceedings of the Conference, pages 135-142, Vancouver, Canada, June 1989. Association for Computational Linguistics.
- [11]
- H. Leiß. Bounded fixed-point definability and tabular recognition of languages. In Computer Science Logic. 9th International Workshop, CSL'95., volume 1092 of LNCS, pages 388-402. Springer, 1996.
- [12]
- H.R. Lewis and C.H. Papadimitriou. Elements of the theory of computation. Prentice Hall, snd edition, 1998.
- [13]
- S. Naumann and H. Langer. Parsing. Teubner, Stuttgart, 1994.
- [14]
- M.-J. Nederhof. Linguistic Parsing and Program Transformation. PhD thesis, Proefschrift Nijmegen, Wiskunde en Informatica, 1994.
- [15]
- M.-J. Nederhof and G. Satta. Efficient tabular LR parsing. In Proceedings of the 34th Annual Meeting of the ACL, pages 239-246, Morristown, NJ, USA, 1996. Association for Computational Linguistics.
- [16]
- A. Okhotin. Boolean grammars. Information and Computation, 194(1):19-48, 2004.
- [17]
- E. Rich. Automata, Computability, and Complexity: Theory and Applications. Prentice-Hall, 2007.
- [18]
- U. Schöning. Theoretische Informatik - kurzgefaßt. Hochschultaschenbuch. Spektrum Akademischer Verlag GmbH, Heidelberg-Berlin, 2000.
- [19]
- E. Scott, A. Johnstone, and R. Economopoulos. BRNGLR: a cubic Tomita-style GLR parsing algorithm. Acta Inf., 44(6):427-461, 2007.
- [20]
- S. Sippu and E. Soisalon-Soininen. Parsing Theory. Vol.I: Languages and Parsing. EATCS Monographs on Theoretical Computer Science. Springer-Verlag, Berlin, 1988.
- [21]
- M. Tomita. Efficient Parsing for Natural Language: A Fast Algorithm for Practical Systems. Kluwer Academic Publishers, Norwell, MA, USA, 1985.
- [22]
- I. Wegener. Theoretische Informatik. Teubner, 1993.
- [23]
- Terry Winograd. Language as a Cognitive Process, Volume 1: Syntax. Addison Wesley, New York, 1983.
- [24]
- D. H. Younger. Recognition and parsing of context-free languages in time n3. Information and Control, 10(2):372-375, 1967.
Footnotes:
1The expert reader may have a look at the example first to spot the modifications in comparison to "their textbook version" of CYK.
2Note that if a subword v occurs several times in w, computing and storing Tv for each occurrence (i,j) separately wastes some time and space. There may be applications where it pays off to implement T as an array indexed by subwords.
3http://www.tcs.ifi.lmu.de/SeeYK
Comments


