Hardware for Basic Arithmetic Operations as a Subject of Computer Science Courses in High Schools
Philipp Kersting
Ingo Wegener
FB Informatik, LS 2
Universität Dortmund
D-44221 Dortmund, Germany
E-Mail: philipp.kersting@gmx.de, wegener@ls2.cs.uni-dortmund.de
Abstract:
Many people working with computers know much about the software. However, their knowledge on the basic hardware components is restricted. Most people are convinced that computers do arithmetics as they have learnt it in elementary school. They even think that this is more or less the only reasonable way to perform arithmetics. This is definitely wrong. The presentation of methods used by modern hardware for the basic arithmetic operations opens the mind. It shows that it is sometimes necessary to look for completely different solutions of problems which seem to have only one natural solution. Besides this very general aim it will be argued why it is useful to consider hardware realizations of the basic arithmetic operations in computer science courses of high schools.
Zusammenfassung:
Typischerweise wissen diejenigen, die mit Rechnern arbeiten, zumindestens etwas über die Software, aber meistens gar nichts über die Hardwarekomponenten. Die meisten Menschen sind sicherlich davon überzeugt, dass Rechner arithmetische Aufgaben mit denselben Methoden bearbeiten, wie sie es in der Schule gelernt haben. Ja, wahrscheinlich glauben sie, dass dies die einzig sinnvollen Methoden sind, die Grundrechenarten auszuführen. Dies ist grundlegend falsch. Daher durchbricht die Diskussion der Methoden, mit denen moderne Hardware Arithmetik realisiert, geistige Schranken. Es zeigt sich, dass es notwendig ist, nach gänzlich neuen Lösungswegen zu suchen - selbst dann, wenn man glauben mag, dass es nur einen natürlichen Lösungsweg gibt. Darüber hinaus werden viele konkrete Argumente vorgestellt, warum und wie es sinnvoll ist, Hardwarerealisierungen der Grundrechenarten bereits in der Schule zu diskutieren.
- 1. Introduction
- 2. How humans and computers perform the basic aithmetic operations
- 3. Adder
- 4. Subtraction
- 5. Multipliers
- 6. Dividers
- 7. Some aspects of the verification of circuits
- 8. Some didactic aspects
- 9. Conclusions
- References
- Appendix
1. Introduction
Some years ago the new Pentium processor was delivered and a customer found out that the processor computed wrong results for some division problems. Indeed, for most inputs the divider worked correctly - but not for all. This fault has become well known as the Pentium bug. The cost to renew all processors was around 450 million dollars. How is it possible that computers solve very difficult problems and err on a problem which humans learn to solve in elementary school? Why has the bug not been found during the testing process? Is it possible to verify (in a formal sense) that a processor works correctly?
In order to discuss all these highly relevant questions one has to understand how the Pentium divider works. The first essential message is that the Pentium divider is not a hardware implementation of the school method of division. We strongly believe that it should be common knowledge that hardware realizations of the basic arithmetic operations differ from the school methods for these operations. Schoolgirls and schoolboys do not learn division as an abstract problem and the school method as a special algorithm for the solution of this problem. Division is "defined" by the division algorithm known as the school method for division. The same holds for addition, subtraction, and multiplication.
In Section 2, we discuss why algorithms for the basic arithmetic operations which are useful for humans have to differ from algorithms useful for hardware realizations. This includes an important learning goal. Solutions can be considered as good, useful or efficient only if one has agreed on the aims, more precisely on the criteria to evaluate the solutions. It will be surprising to learn that this is already true for methods to add numbers. In order to design an essentially new solution it is necessary (independent from the problem) to overcome the usual way of thinking. The consideration of adders, multipliers, and dividers different from the school methods supports such creative thinking.
Moreover, this subject supports algorithmic thinking and considers many algorithmic properties, e.g., divide-and-conquer, dynamic programming, recursion, and approximization. In particular, one directly is confronted with the problem of parallelization and the analysis of the efficiency of algorithmic solutions. All these issues are discussed for problems which "obviously" are important. It is easy to introduce the subject, since the problems are "well known". Finally, the subject has the advantage that (most certainly) nobody knows much about the subject in advance.
We present the main principles of algorithms for the basic arithmetic operations. Many of the technical details are presented in the appendix. In Section 3, we discuss the school method for addition, the carry-look-ahead adder, the conditional sum adder, and the Ladner-Fischer adder. Section 4 contains some short comments on subtraction. Section 5 is devoted to multipliers, i.e., the school method, the Wallace tree, the Karatsuba and Ofman algorithm and the use of redundant number representations. Finally, Section 6 considers dividers, i.e., the school method, Newton's algorithm, the IBM method, and the method leading to the Pentium bug. In all these sections we introduce the main algorithmic ideas and the methods to analyze their efficiency. Details can be found in the monographs Wegener (1987, 1996, 2000) and in journal papers cited in these monographs. We also discuss the didactical aspects of these algorithms. In Section 7, we add some remarks on hardware and software verification, since the Pentium bug was the starting point of our discussion. Some specific didactical issues are discussed in the corresponding sections. In Section 8, we present the general didactical background. We try to argue why the considered subject, hardware realizations of basic algorithmic operations, is a meaningful subject in computer science courses of high schools. We finish with some conclusions.
2. How humans and computers perform the basic arithmetic operations
The considered problems are well known. For given n-bit numbers (more often n-digit numbers for humans) a and b compute a+b, a-b, a.b and a/b (the n most significant bits), resp. The problems obviously are fundamental. The problems are defined in a mathematical form. This implies that this subject does not contain any aspect of formalization or data modeling. Finally, the problems have a simple and well-known solution, the so-called school methods.
For humans solving the arithmetic problems with "pencil and paper", the school methods are unsurpassed. The learner expects them to be "optimal". However, which aspects are important for solutions to be adequate for humans?
The methods have to be efficient or fast with respect to sequential computations. The human brain works in parallel while processing all the information from the sense organs but (almost all) humans cannot process arithmetic problems in parallel. Humans perform one basic operation per step. An addition or multiplication of digits is such a basic operation. However, not each efficient algorithm is useful for humans. Here, efficiency is calculated as the number of basic operations. Many people have already difficulties with the school method for division. (It is a nice experiment to ask people on the street to calculate 53701 : 83 = 647.) A good algorithm for humans has to be simple enough that humans remember the algorithm and can apply it without thinking about it and without having difficulties with its basic operations. The school methods are iterative algorithms with simple modules.
The aspect of simpleness is useful also for hardware realizations but not essential. A simple algorithm supports the design of the processor and makes the design cheaper. However, this is quite unimportant for the mass production of processors. A simple algorithm can simplify the verification. Nevertheless, chip size and number of operations per second are the main issues. Chip size is closely related to the number of basic operations which are binary operations on boolean inputs, e.g., AND, OR, NOT, EXOR. Hence, as for humans we try to minimize the number of basic (boolean) operations. Hardware works in parallel. Operations can be performed in parallel if all inputs of the operation are available. This leads to the model of a (combinational or boolean) circuit which includes all important issues.
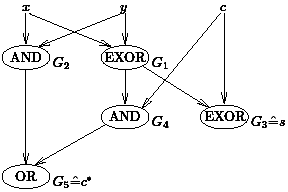
A circuit is a directed acyclic graph with inputs (no incoming edges) representing boolean variables and constants, and gates (one or two incoming edges and a gate type like NOT for a gate with one incoming edge and AND, OR, or EXOR for two incoming edges). The gates are numbered sequentially, i.e., an edge leading from Gi to Gj implies i<j. Some gates are declared as output gates. The sequential computation is a gate-by-gate computation. For an actual input the inputs of a circuit all realize boolean values. If we know the values realized at G1,..., Gi-1, we know the input values of Gi and can apply the boolean operation corresponding to Gi to these values in order to obtain the value realized at Gi. The example in Figure 1 implements a full adder for the bits x and y and the carry c. The outputs are the sum bit s and the new carry c*.
|
Figure 1: A circuit realisation of a full adder. |
The circuit size is a measure of the sequential time complexity and is equal to the number of gates, the example circuit has size 5. Circuit size is a simplified measure for the hardware cost of a circuit. However, G1 and G2 can be evaluated in parallel, all other gates have to "wait", since an input signal is not yet calculated. In Step 2, G3 and G4 can be evaluated and, finally, in Step 3, G5 can be evaluated. Let l (G) be the level of G, i.e., the length of a longest path from some input to G. All gates G where l (G) = i can be evaluated in the ith step and not earlier. The largest l (G) of all output gates is called the depth of the circuit and represents the parallel computation time of the circuit which is a quite realistic but nevertheless simplified (there are delays on wires and at gates) measure for the computation time of a circuit. Circuits should have small size and small depth. However, it is not for all problems possible to minimize size and depth simultaneously.
We have seen that it is quite easy to introduce and motivate the problems. The learner sees that it is important which aims we try to fulfill. Humans and processors prefer solutions with a small number of basic operations but humans prefer a simple algorithm while processors prefer an algorithm leading to small circuit depth. Moreover, the problem has become complicated, since we try to minimize size and depth simultaneously. This is an important issue. Many realistic problems are not classical optimization problems where a function f: S->![]() (S is some set) has to be optimized, e.g., minimized. Often one has to deal with problems f : S->
(S is some set) has to be optimized, e.g., minimized. Often one has to deal with problems f : S-> m (m>1 but not very large) and solutions can be incomparable. If f (a)=(3,4) and f (b)=(6,2) and the aim is minimization, some people may prefer a while others prefer b. The new aim is the following. The best thing is to minimize all coordinates of f (in our case size and depth) simultaneously. If this is not possible, one should present a list of solutions, in the best case for each possible circuit size s a circuit of size s and minimal depth among the circuits of size s. Hence, the learner has to cope with multi-objective optimization in a very natural setting.
m (m>1 but not very large) and solutions can be incomparable. If f (a)=(3,4) and f (b)=(6,2) and the aim is minimization, some people may prefer a while others prefer b. The new aim is the following. The best thing is to minimize all coordinates of f (in our case size and depth) simultaneously. If this is not possible, one should present a list of solutions, in the best case for each possible circuit size s a circuit of size s and minimal depth among the circuits of size s. Hence, the learner has to cope with multi-objective optimization in a very natural setting.
3. Adders
The problem is to compute the sum s=(sn, sn-1,..., s0) of two n-bit numbers x=(xn-1,..., x0) and y=(yn-1,..., y0). The school method for addition (SMADD) works with full adders which we have already discussed as an example circuit in Section 2 (see Figure 1). At position 0 there is no carry and it is sufficient to use a half adder consisting of the gates G1 and G2 of a full adder. It is easy to analyze the school method. A full adder has size 5 and depth 3 and a half adder has size 2 and depth 1. Hence, the total size equals
SIZESMADD(n)=5n-3.
The full adders work sequentially, since the full adder at position i has to wait for the carry ci-1 from position i-1. This leads to an upper bound of 3n-2 for the depth. However, ci-1 is used not before level 2 of the full adder at position i (see Figure 1). The gates G1 and G2 of all copies of the full adder can be evaluated in parallel in the first step. Afterwards, the full adders need only two further steps proving that
DEPTHSMADD(n)=2n-1.
The investigation of the school method for addition is very simple and one learns to work with circuits. Moreover, we can discuss the results. The output bit sn depends on all 2n input bits. Since all basic operations combine only two signals, 2n-1 gates are necessary to compute sn-1. This shows that linear size is the best we can hope for. Hence, the school method for addition has all issues of a good solution for humans. Indeed, one can mention that it has been proved that 5n-3 is the optimal size of adders, i.e., an adder with 5n-4 gates is impossible.
The depth of the school method for addition is roughly by a factor of 2.5 smaller than its size. Hence, it is not a purely sequential solution. Is linear depth a satisfactory solution? The answer is no. A background information: Each boolean function on n variables can be realized by its DNF (disjunctive normal form) with depth n+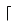 log n
log n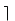 . For teaching the following example is instructive. Compute the disjunction (OR) of n inputs. The above considerations show that size n-1 is necessary. Using a balanced binary tree we obtain a solution with optimal size n-1 and depth
. For teaching the following example is instructive. Compute the disjunction (OR) of n inputs. The above considerations show that size n-1 is necessary. Using a balanced binary tree we obtain a solution with optimal size n-1 and depth 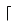 log n
log n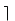 (a simple argument shows that
(a simple argument shows that 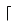 log n
log n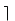 is optimal, since binary trees with n leaves need depth
is optimal, since binary trees with n leaves need depth 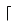 log n
log n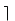 ). This leads to the aim to obtain depth bounds which are small with respect to log n where n is the length of the input. The school method for addition has a large depth and is inadequate for hardware solutions.
). This leads to the aim to obtain depth bounds which are small with respect to log n where n is the length of the input. The school method for addition has a large depth and is inadequate for hardware solutions.
The first idea is to start with the school method and to partition it into three modules in order to see which part is hard to parallelize. Step 1 consists of n parallel half adders computing ui=xi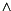 yi and vi=xi
yi and vi=xi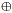 yi(
yi( 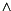 = AND,
= AND, 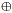 = EXOR), size 2n, depth 1. Step 2 computes the carry bits cn-1,..., c0. This is the hard part. Step 3 computes the sum bits where s0=v0 (no carry at position 0), sn=cn-1 (the carry of the addition) and si=vi
= EXOR), size 2n, depth 1. Step 2 computes the carry bits cn-1,..., c0. This is the hard part. Step 3 computes the sum bits where s0=v0 (no carry at position 0), sn=cn-1 (the carry of the addition) and si=vi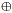 ci-1, 1
ci-1, 1 i
i n-1, since si is the EXOR-sum (the less significant bit) of xi, yi and ci-1, size n-1, depth 1.
n-1, since si is the EXOR-sum (the less significant bit) of xi, yi and ci-1, size n-1, depth 1.
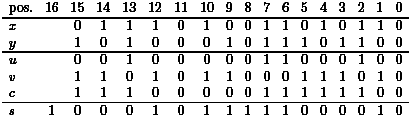
Here we have applied the principle of problem modularization. Now we discuss how carries are produced. The following example is illustrative and will be used as the running example of this section.
|
Figure 2: The addition of x and y, the results u and v of the half adders, the carry bits c and the sum bits s. |
Now we can discuss how addition works. At position i, there are four different inputs, namely (0,0), (0,1), (1,0), and (1,1). The result is the same for (0,1) and (1,0). The pair (ui,vi) contains the essential information :
- (xi,yi)=(0, 0)
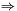 (ui, vi)=(0, 0). Such a position is called E, since it eliminates carries from the previous positions. The partial sum is 0 and even a carry from the previous positions cannot produce a carry at this position.
(ui, vi)=(0, 0). Such a position is called E, since it eliminates carries from the previous positions. The partial sum is 0 and even a carry from the previous positions cannot produce a carry at this position. - (xi,yi)= (0,1) or(xi,yi)=(1,0)
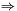 (ui,vi)=(0,1). Such a position is called P, since it propagates carries from the previous positions. The partial sum is 1 and we obtain a carry at this position if and only if we obtain a carry from the previous positions.
(ui,vi)=(0,1). Such a position is called P, since it propagates carries from the previous positions. The partial sum is 1 and we obtain a carry at this position if and only if we obtain a carry from the previous positions. - (xi,yi)=(1,1)
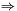 (ui,vi)=(1,0). Such a position is called G, since it generates a carry. The partial sum is 2 and this implies that we have a carry at this position.
(ui,vi)=(1,0). Such a position is called G, since it generates a carry. The partial sum is 2 and this implies that we have a carry at this position.
Moreover, vi=1 indicates a P-position and ui=1 indicates a G-position. How do we obtain a carry at position i ? We only have to consider the positions to the right including position i. We start at position i and walk to the right until we find a position of type E or G. If we find E, then we have P...PE with some number of P's. There is no carry at the E-position implying that all other considered positions do not produce carries. If we find G, then we have P...PG. There is a carry at the G-position implying that this carry is propagated to all the considered positions. If we find neither E nor G, all considered positions are of type P. There is no carry from (the not existing) position -1 and we have no carry at the considered position. Hence, we get a more illustrative version of Figure 2.
|
Figure 3: Figure 2 revisited showing the "type" of the positions. |
Now it is easy to see that the carries at the position 15, 14, and 13 are generated at position 13 and then propagated. The G-position 7 generates a carry at position 7 which is eliminated at position 8, the G-position 6 generates a carry for this position. Finally, the G-position 2 generates a carry at position 2 which is propagated to the positions 3, 4, and 5. This example directly leads to an algorithmic idea:
- There exists a carry at position i if and only if there exists some j
 i such that position j is of type G and all positions j+1,..., i are of type P.
i such that position j is of type G and all positions j+1,..., i are of type P.
Remembering how G- and P-positions can be identified and using the fact that "there exists" can be described as boolean disjunction OR (denoted by the symbol 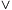 ) we obtain the formula
) we obtain the formula
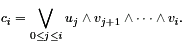
This formula is the core of the so-called "carry-look-ahead" adder (CLA). The carry cn-1 has the "largest" formula. However, we can recycle the idea of using balanced trees for the computation of ANDs, ORs, or EXORs. Each conjunction (AND) uj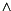 vj+1
vj+1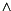 ...
... 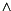 vi consists of at most n terms and can be realized in depth
vi consists of at most n terms and can be realized in depth 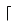 log n
log n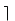 . The same holds for the disjunction (OR) of the resulting terms. Adding the depth for the other two steps of our general approach we get
. The same holds for the disjunction (OR) of the resulting terms. Adding the depth for the other two steps of our general approach we get
DEPTHCLA(n) = 2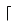 log n
log n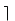 + 2
+ 2
which is a remarkable improvement in comparison to the school method. What about the size of this approach? Let us consider ci-1. We need i-1 OR-gates to combine the i terms. The AND-terms need 0, 1,..., i-1 AND-gates respectively. Altogether, ci-1 needs a size of approximately i2. It is possible to compute the precise result:
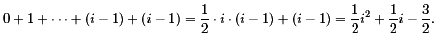
We have to consider the total size of the computation of all ci. The size is of order n3, the leading term is 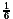 n3 (the sum of all
n3 (the sum of all ![]() i2). These calculations can be simplified. There are n/2 terms all larger than
i2). These calculations can be simplified. There are n/2 terms all larger than 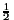 (
(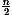 )2 =
)2 = 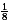 n2 leading to a lower bound of
n2 leading to a lower bound of 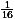 n3. There are n terms all smaller than
n3. There are n terms all smaller than 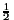 n2 +
n2 + 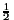 n leading to an upper bound of
n leading to an upper bound of 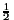 n3 +
n3 + 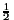 n2. Cubic size is not acceptable for the hardware realization of adders. The learner is confronted with a size-depth trade-off if she or he compares the school method with the carry-look-ahead method.
n2. Cubic size is not acceptable for the hardware realization of adders. The learner is confronted with a size-depth trade-off if she or he compares the school method with the carry-look-ahead method.
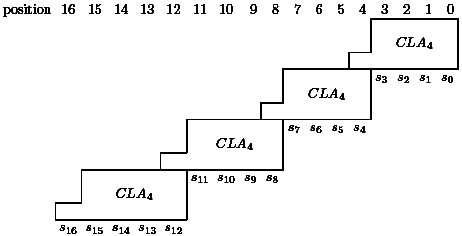
Here we have a typical situation in computer science. Methods in their pure form have some good properties but also bad properties. Better solutions can often be obtained as compromises. Let n=2k and m=2l<n. We obtain an n-bit-adder by using a carry-look-ahead adder for the last m bit positions which also leads to the carry for the next block of m positions where again a carry-look-ahead adder is used.
|
Figure 4: A hybrid adder combining ideas from the school method and the pure carry-look-ahead adder. |
It is useful to play with parameters in order to determine size and depth for different values of n and m. In general, there are n/m blocks which work sequentially and which are pure carry-look-ahead adders for parameter m. The total depth is
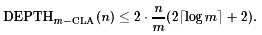
It is sufficient to approximate the total size: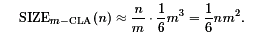
Here it is useful to discuss that a closer look leads to some improvements for the estimation of the necessary resources. The first steps of all CLAm-blocks can be realized in parallel and the carry for the next block is produced already in the last but one step of the previous block. However, it is also useful to discuss that it is not necessary to obtain exact results on size and depth in order to discuss the advantages and disadvantages of a method.
The Ladner-Fischer method (LF) is based on one further idea. We have used the fact that each position is one of the types E, P, or G. Now we consider E, P, and G as functions taking as an input the carry bit c from the previous position and computing the carry bit of the current position. It follows by case inspection that
| E(c) | = | 0, | |
| P(c) | = | c, and | |
| G(c) | = | 1. |
For functions the operation composition denoted by "o" is well defined. We are lucky that the composition of the functions E, P, and G leads to a function E, P, or G. We have
- EoE = EoP = EoG = E, since an eliminate position eliminates the influence of previous positions,
- GoE = GoP = GoG = G for similar reasons, and
- PoE = E, PoP = P, andPoG = G, since P is the identity function.
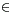 {E,P,G} be the type of the i-th position. Then Bi=Aio ... oA0 contains the full information on carries, namely ci=Bi(0), since there is no carry to position 0. Hence, ci=1 if Bi=G.
{E,P,G} be the type of the i-th position. Then Bi=Aio ... oA0 contains the full information on carries, namely ci=Bi(0), since there is no carry to position 0. Hence, ci=1 if Bi=G.
In order to compute Bi we have to solve two problems. The first one is a typical hardware problem. How can we realize "o"? Let A, A'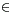 {E,P,G} be given by (u,v) and (u',v'), respectively. Remember that
{E,P,G} be given by (u,v) and (u',v'), respectively. Remember that
- (u,v)=(0,0) if A=E,
- (u,v)=(0,1) if A=P, and
- (u,v)=(1,0) if A=G.
The task is to compute the coding (u",v") of A"=AoA'. This problem can be solved by complete case inspection, since we only have four input bits. Since (u,v)=(1,1) is not possible, there are only nine different inputs. However, we may argue directly. The result v"=1 has to indicate that A"=P but A"=P if and only if A=P and A'=P which leads to v"=v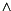 v'. The result u"=1 has to indicate that A"=G which is equivalent to A=G or (A=P and A'=G). Hence, u"=u
v'. The result u"=1 has to indicate that A"=G which is equivalent to A=G or (A=P and A'=G). Hence, u"=u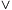 (v
(v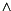 u'). The circuit for "o" has size 3 and depth 2. Moreover, we should realize that the composition of functions is an associative operation. This is perhaps already known or considered as obvious or can be shown in our special situation by case inspection to show that Ao(A'oA") = (AoA')oA". Now we have to solve the so-called prefix problem (which here is a suffix problem). Given An-1,..., A0
u'). The circuit for "o" has size 3 and depth 2. Moreover, we should realize that the composition of functions is an associative operation. This is perhaps already known or considered as obvious or can be shown in our special situation by case inspection to show that Ao(A'oA") = (AoA')oA". Now we have to solve the so-called prefix problem (which here is a suffix problem). Given An-1,..., A0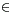 {E,P,G} we have to compute all Bi=Aio ... oA0. We consider "o" as a basic circuit operation which later is replaced by the small circuit constructed above. We are interested in a solution with small size and depth. This is an interesting problem. Moreover, this problem has many further applications for the parallelization of algorithms. The solution is a simple recursive algorithm based on the simple fact that Bi = AioBi-1. We consider the algorithm only for n=2k (the typical situation in hardware):
{E,P,G} we have to compute all Bi=Aio ... oA0. We consider "o" as a basic circuit operation which later is replaced by the small circuit constructed above. We are interested in a solution with small size and depth. This is an interesting problem. Moreover, this problem has many further applications for the parallelization of algorithms. The solution is a simple recursive algorithm based on the simple fact that Bi = AioBi-1. We consider the algorithm only for n=2k (the typical situation in hardware):
Step 1:
compute Ci=A2i+1oA2i, 0 i
i n/2-1,
n/2-1,
Step 2:
solve the prefix problem for C0,..., Cn/2-1 leading to D0,..., Dn/2-1 where Di=Cio...oC0=A2i+1oA2io...oA1oA0=B2i+1
Step 3:
compute the missing results B2i=A2ioB2i-1 where B0=A0 is already given.
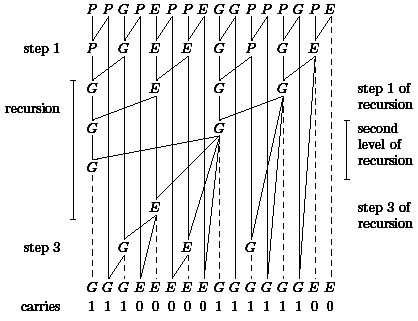
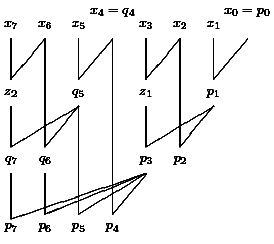
We illustrate this algorithm for n=16 and our example.
|
Figure 5: The prefix algorithm for n = 16. |
Here the learner sees that the hardware realization is the iterated version of the considered recursive algorithm. The recursive version is adequate for the analysis of the algorithm. Step 1 and Step 3 need depth 1 each and the common size of these steps equals n-1. We simplify the analysis by estimating the size by n. Step 2 is an application of the algorithm for input size n/2. Hence, the total size is bounded by
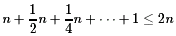
and the recursion depth is log n leading to a total depth of 2 log n. Inserting the small circuits for "o" the size is bounded by 6n and the depth by 4 log n. We have to take into account the half adders and the final computation of the sum bits. The final result is
 9n and
9n and DEPTHLM(n)  4 log n + 2.
4 log n + 2.
It is worthwhile to mention that a more complicated prefix algorithm halves the depth at the cost of doubling the size.
Altogether, we have designed with simple methods an adder which leads to a very efficient hardware solution. It has simultaneously linear size and logarithmic depth. It has a regular structure (see Figure 5) simplifying the hardware realization. Everyone will agree that the Ladner-Fischer method is not useful for humans, since it is already too complicated. Moreover, the number of basic operations is by 80% larger than for the school method.
Another adder may be introduced to discuss the risk if recursive algorithms are used without further thinking. We discuss the conditional sum adder (CS) in the appendix A1.
Altogether, addition is an operation with an amazing variety of possible solutions. Teaching these methods has the advantage of presenting many different fundamental methods.
4. Subtraction
Subtraction is closely related to addition. It is only an exercise to transfer the methods for addition to work for subtraction namely the computation of a-b for n-bit numbers a and b where a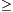 b. We just have to work with another type of carry. The situation is more complicated if we allow negative integers as inputs. The usual representation by a sign bit and the absolute value of the number leads to the consideration of different cases. It is possible to use this subject for the introduction of alternative representations of numbers like the 2-complement representation. This representation has the advantage of allowing a unified approach for the subtraction of positive and negative integers. It is useful to teach the fact that the binary and the decimal representation of numbers (with sign bit) are not the only useful representations of integers. We omit the details.
b. We just have to work with another type of carry. The situation is more complicated if we allow negative integers as inputs. The usual representation by a sign bit and the absolute value of the number leads to the consideration of different cases. It is possible to use this subject for the introduction of alternative representations of numbers like the 2-complement representation. This representation has the advantage of allowing a unified approach for the subtraction of positive and negative integers. It is useful to teach the fact that the binary and the decimal representation of numbers (with sign bit) are not the only useful representations of integers. We omit the details.
5. Multipliers
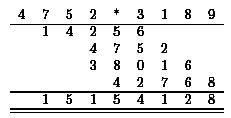
First, we discuss some issues of the school method for multiplication applied to decimal numbers. Figure 6 shows an example.
|
Figure 6: The school method for multiplication. |
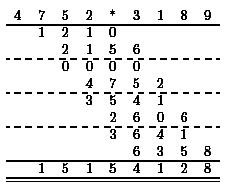
We multiply the first number by each digit of the second number, perform the appropriate shifts, and compute the sum of the resulting numbers. All empty entries in Figure 6 implicitly represent zeros. In order to parallelize this algorithm we already have difficulties with the carries generated during the multiplication of numbers by digits. It is useful to introduce already here a trick which also is used later. We represent the result of the multiplication of a number by a digit by two numbers whose sum is the real result. The first number consists of the carries and the second one of the other digits, see Figure 7.
|
Figure 7: The school method for multiplication revisited. |
The crucial fact is that we now can multiply each digit of the first number by each digit of the second number in parallel. Hence, the first step can be performed in depth 1. Afterwards, we have to compute the sum of 2n instead of n numbers. This method also can be interpreted in the following way. We multiply the first number (4752) by a digit, i.e., 8, and the result is not the unique decimal representation of the product but a redundant representation of the product namely by two numbers whose sum is equal to the considered product. Hence, the result is only an intermediate one but the parallel execution time has been reduced significantly. The message is the following one. It may be useful to work with redundant number representations and to transform the result only in the last step into the unique representation by decimal numbers.
However, in the case of binary numbers the multiplication of numbers by bits cannot lead to carries and this step is easy. Afterwards, we have to compute the sum of n (2n-1)-bit numbers where many positions are known to be equal to 0. In particular, it is known that the result is a (2n)-bit number. Here we describe the methods without the discussion what can be saved because of the fixed 0-entries. For these details see Wegener (1996).
The school method for the addition of n numbers has to deal with the problem of carries and these problems are more difficult than for adders working on two numbers. Hence, a good idea is to reduce the problem to subproblems which have been solved before - the addition of two numbers. In a first step we consider the addition of two numbers as a basic operation. The addition of n numbers can be realized by a balanced tree with n-1 operations and depth log n (in order to simplify the discussion we assume that n=2k). Each basic operation can be replaced by a Ladner-Fischer adder of size 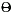 (n) (
(n) (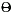 describes the growth order precisely, O describes an upper bound and
describes the growth order precisely, O describes an upper bound and 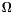 a lower bound) and depth
a lower bound) and depth 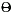 (log n). The whole method is called SMLF (school method with Ladner-Fischer adders) and
(log n). The whole method is called SMLF (school method with Ladner-Fischer adders) and
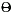 (n2)
(n2)DEPTHSMLF(n) = 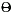 (log2n).
(log2n).
(In this and the following section we simplify the presentation and consider only the growth order of the size and the depth of circuits. It is easy but a little bit tedious to obtain more precise results (see Wegener (1996)).
The method SMLF is quite efficient and it seems hard to beat these bounds. It seems to be necessary to multiply each pair of bits leading to n2 basic operations. It also seems to be necessary to compute the sum of nn-bit numbers. An adder for two n-bit numbers needs depth ![]() log(2n)
log(2n)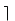 . Nevertheless, a simple but clever idea is sufficient to beat the depth bound - even without increasing the size.
. Nevertheless, a simple but clever idea is sufficient to beat the depth bound - even without increasing the size.
The method is based on the idea discussed at the beginning of this section: the use of redundant number representations. Let add (p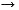 q) denote the problem to compute the sum of p numbers of bit length at most 2n where the result can be represented by at most q numbers whose sum equals the sum of the given p numbers. We are faced with the problem add (n
q) denote the problem to compute the sum of p numbers of bit length at most 2n where the result can be represented by at most q numbers whose sum equals the sum of the given p numbers. We are faced with the problem add (n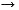 1). The basic operation add (2
1). The basic operation add (2 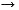 1) needs depth
1) needs depth ![]() log(2n)
log(2n)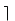 . However the problem add (3
. However the problem add (3 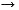 2) can be solved in depth 3. We use a so-called carry save adder (CSA gate) which consists of full adders for each bit position. The first number of the result consists of the sum bits and the second number consists of the carries. Using n-2 CSA gates whose size altogether is
2) can be solved in depth 3. We use a so-called carry save adder (CSA gate) which consists of full adders for each bit position. The first number of the result consists of the sum bits and the second number consists of the carries. Using n-2 CSA gates whose size altogether is 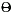 (n2) we reduce the number of summands from n to 2. The sum of the resulting two numbers is computed by a Ladner-Fischer adder. What about the depth of this approach? If we have 3m+i, 0
(n2) we reduce the number of summands from n to 2. The sum of the resulting two numbers is computed by a Ladner-Fischer adder. What about the depth of this approach? If we have 3m+i, 0 i
i![]() 2, summands, we can apply m CSA gates in parallel and obtain 2m+i summands. Hence, the number of summands is roughly reduced by a factor of 2/3 and we expect that the depth with respect to CSA gates is approximately log3/2n (remember that
2, summands, we can apply m CSA gates in parallel and obtain 2m+i summands. Hence, the number of summands is roughly reduced by a factor of 2/3 and we expect that the depth with respect to CSA gates is approximately log3/2n (remember that 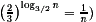 ). An easy calculation shows that depth
). An easy calculation shows that depth 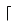 log3/2n
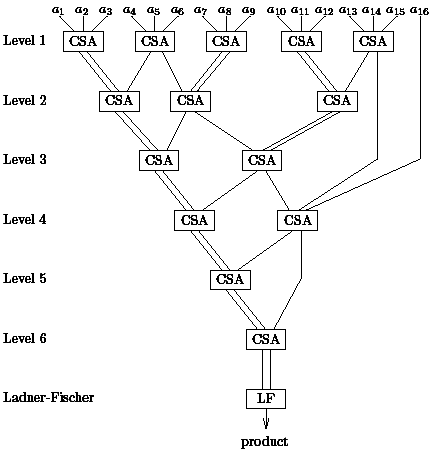
log3/2n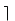 is sufficient. Figure 8 shows an example of this method for n=16.
is sufficient. Figure 8 shows an example of this method for n=16.
|
Figure 8: The school method for multiplication with Wallace trees. |
Since the basic method is still the school method, we call this method SMWT (school method for multiplication with Wallace trees). The graph of CSA gates is known as Wallace tree. This notion is questionable, since the Wallace tree is not a tree. Nevertheless, this notion is common. It is obvious that
SIZESMWT(n) = 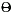 (n2)
(n2)
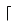 log3/2n
log3/2n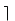 (since CSA gates have depth 3) and the smallest depth of a Ladner-Fischer adder for (2n)-bit numbers equals 2
(since CSA gates have depth 3) and the smallest depth of a Ladner-Fischer adder for (2n)-bit numbers equals 2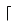 log n
log n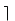 + 4. Hence,
+ 4. Hence,DEPTHSMWT(n) = 2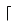 log n
log n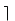 + 3
+ 3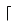 log3/2n
log3/2n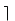 + 5
+ 5 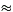 7.13 log n + O(1).
7.13 log n + O(1).
This simple design of an efficient multiplier shows that we have to escape from well-established thought patterns in order to obtain unconventional designs which are better than "obviously insurmountable bounds".
Another "obviously insurmountable bound" is the n2-bound for the size. In A2 we show how to beat this "obvious" bound.
The conclusion is: Doubt any bound which has not been proved! Schönhage and Strassen have designed a multiplier of size 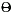 (n log n loglog n) which for large n is the nowadays most efficient multiplier. A software implementation of this implementation has real applications. There are almost no hardware implementations of this method, since this method is only used for the multiplication of n-bit numbers where n=512, 1024, or even 2048. Who needs such large numbers? Everybody who likes to use computers for e-commerce or e-cash and everybody who uses the computer for private communication. Then messages have to be enciphered and deciphered and messages have to be signed by digital signatures. Modern public key cryptography works with very long numbers as considered above.
(n log n loglog n) which for large n is the nowadays most efficient multiplier. A software implementation of this implementation has real applications. There are almost no hardware implementations of this method, since this method is only used for the multiplication of n-bit numbers where n=512, 1024, or even 2048. Who needs such large numbers? Everybody who likes to use computers for e-commerce or e-cash and everybody who uses the computer for private communication. Then messages have to be enciphered and deciphered and messages have to be signed by digital signatures. Modern public key cryptography works with very long numbers as considered above.
However, there is still a problem. The algorithms of Karatsuba/Ofman and Schönhage/Strassen beat the school method only for quite large n, e.g., n>64 for Karatsuba/Ofman and n very large for Schönhage/Strassen (see Wegener(1996)). It is not useful to apply the new methods in pure form. Both methods are divide-and-conquer algorithms. Hence, we can solve subproblems which are small enough with another method. Karatsuba and Ofman's "mixed" method beats the school method for n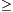 16. The best application of the algorithm due to Schönhage and Strassen is to switch for small enough subproblems to the Karatsuba and Ofman method which itself switches for small enough subproblems to the school method. This combination of methods is a typical idea for real applications. Multiplication is perhaps the simpliest example for this essential trick.
16. The best application of the algorithm due to Schönhage and Strassen is to switch for small enough subproblems to the Karatsuba and Ofman method which itself switches for small enough subproblems to the school method. This combination of methods is a typical idea for real applications. Multiplication is perhaps the simpliest example for this essential trick.
The interested reader asks for the depth of the new methods. The algorithm of Karatsuba and Ofman first performs two multiplications recursively, then three additions, then another multiplication, and finally a subtraction. This makes it hard to work with CSA gates. It would be better to have a redundant number representation which allows the addition and subtraction of two numbers in constant depth. We introduce in A3 such a representation, the so-called radix-4 representation. This is an advanced topic for high school courses. Nevertheless, it is an interesting topic and this type of number representation is used in modern computers (see the Pentium divider in the next section).
The multiplication of very large numbers is nowadays a very important operation and can be performed very quickly with methods different from the school method for multiplication. The consideration of these methods includes the introduction of different redundant number representations (sum of two numbers, radix-4), the parallelization by balanced trees (binary trees and Wallace trees), divide-and-conquer, and also the investigation of mixed forms of different algorithms.
6. Dividers
We have claimed in Section 2 that the school method for division is much more difficult than the school methods for the other basic arithmetic operations. Confronted with the task to compute 53701 : 83 one has to "guess" that 6.83 ![]() 537 but 7.83>537. Then one has to compute 537-6.83=39 and has to solve the remaining task 3901:83. The school method is an iterative algorithm (a simple loop) which seems to be inherently sequential. The number of loop traversals is at most n, each loop traversal consists of the "right guess" of the next digit of the quotient (one may try each of the 10 digits or may use binary search), a multiplication of a digit by the divisor and a subtraction. Hence, we may estimate the size by
537 but 7.83>537. Then one has to compute 537-6.83=39 and has to solve the remaining task 3901:83. The school method is an iterative algorithm (a simple loop) which seems to be inherently sequential. The number of loop traversals is at most n, each loop traversal consists of the "right guess" of the next digit of the quotient (one may try each of the 10 digits or may use binary search), a multiplication of a digit by the divisor and a subtraction. Hence, we may estimate the size by 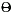 (n2) and the depth by
(n2) and the depth by 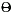 (n log n). Everything gets easier for binary numbers. The multiplication of a bit by the divisor is trivial and we only have to try whether 1 is the next bit of the quotient. However, this does not change the asymptotic results and
(n log n). Everything gets easier for binary numbers. The multiplication of a bit by the divisor is trivial and we only have to try whether 1 is the next bit of the quotient. However, this does not change the asymptotic results and
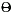 (n2),
(n2), DEPTHSMDIV(n) = 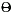 (n log n).
(n log n).
The example 53701:83 has the property that the result is an integer. Usually we have the problem of rounding. We look for the n most significant digits or bits of the quotient and apply some rounding rule. We are faced with the problem to compute an approximation of the exact result and have to cope with numerical problems. Hence, mathematical results on approximation can be applied. If a is a lower bound and b is an upper bound for the quotient, we can check by multiplication whether (a+b)/2 is an upper or a lower bound. This method of nested intervals halves the interval containing the quotient with each step. We are computing one bit of the quotient per step. This is too expensive, since we need an approximation method with a much better rate of convergence. Here it is possible to show that calculus has applications in computer science. Newton's method is described in A4.
Another approximation method is the so-called IBM method which has the same asymptotic depth O(log2n) and a size which is by a factor of O(log n) larger than the size of the multiplier which is used. This method is described in A5.
The only known dividers whose depth is O(log n) are of theoretical interest only, since their depth is only for very large n smaller than the depth of the considered O(log2n) dividers. Hardware dividers work with numbers whose bit length is bounded by 128 and most often by 64. If n=64, log n=6 and log2n=36. Hence, constant factors and additive terms play a major rule. This opens a discussion when and why assymptotic results are of interest. For fixed n (not too large) the school method for division is a serious opponent to the other dividers.
The Pentium divider is a very clever variant of the school method. Not all design details are known but we can be sure that the following radix-4 SRT divider follows the same design principles as the Pentium divider. The design principles have been described in 1968 proving that (even in computer science) fundamental ideas do not become antiquated quickly. In the following we discuss essential features of this divider. The algorithm works in rounds and in each round one "piece" of the result is produced. Hence, the method cannot avoid that the depth grows linearly with the length of the result. It is efficient for numbers which are not too long, since each round can be realized very efficiently.
The school method has to consider the whole dividend and the whole divisor in order to compute the next bit of the quotient. Here the result is represented as a radix-4 number (see A3). Because of the redundancy of radix-4 representations it turns out to be sufficient to work with a small part of the divisor d and a small part of the remainder r (which initially is the dividend). With some appropriate shifts we can ensure that 1  d < 2 and 1
d < 2 and 1  r < 2. This implies that the essential invariant of this method namely
r < 2. This implies that the essential invariant of this method namely
-8 . d 3 . r
3 . r 8 . d
8 . d
is fulfilled in the beginning. This invariant is essential for the following reason. The "pieces" of a radix-4 representation are elements qi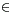 { - 3, - 2, - 1, 0, + 1, +2, + 3} and we have to multiply qi by d in order to compute the new remainder. This is trivial or a shift ifqi
{ - 3, - 2, - 1, 0, + 1, +2, + 3} and we have to multiply qi by d in order to compute the new remainder. This is trivial or a shift ifqi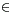 { - 2, - 1, 0, + 1, + 2} and more expensive ifqi
{ - 2, - 1, 0, + 1, + 2} and more expensive ifqi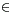 { - 3, + 3}. Hence, only values fromqi
{ - 3, + 3}. Hence, only values fromqi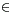 { - 2, - 1, 0, + 1, + 2} are allowed. This implies that r/d has to be bounded by the largest number representable by these entries. The largest number consists of entries 2 only. Since only the positions i
{ - 2, - 1, 0, + 1, + 2} are allowed. This implies that r/d has to be bounded by the largest number representable by these entries. The largest number consists of entries 2 only. Since only the positions i 0 are allowed, the largest number is the sum of all 2.4i, i
0 are allowed, the largest number is the sum of all 2.4i, i 0, which equals 8/3. In the same way we obtain the lower bound -8/3. Both inequalities together lead to the described invariant.
0, which equals 8/3. In the same way we obtain the lower bound -8/3. Both inequalities together lead to the described invariant.
If we choose q0=2, the largest representable number still is 8/3, the smallest number is -8/3+4=4/3. In a similar way we obtain:
- q0=2 is only allowed if 4d
 3r
3r  8d,
8d, - q0=1 is only allowed if d
 3r
3r  5d,
5d, - q0=0 is only allowed if -2d
 3r
3r  2d,
2d, - q0=-1 is only allowed if -5d
 3r
3r  - d,
- d, - q0=-2 is only allowed if -8d
 3r
3r  - 4d.
- 4d.
The intervals [- 8d, - 4d], [- 5d, - d], [- 2d, 2d], [d, 5d], and [4d, 8d] are overlapping because of the redundancy of the chosen number representation. This leads to the idea that it is not necessary to know r and d precisely in order to choose a value of q0 which is one of the possible correct values. Hence, we only consider some short prefixes of r and d. What is the shortest length allowing a correct divider? The radix-4 SRT divider works with prefixes of the remainder consisting of 7 bits (the sign bit and 3 further bits to the left and to the right of the binary point) and with prefixes of the divisor consisting of 5 bits (one bit to the left of the binary point which always equals 1). Hence, there are only 128 "types of remainders" and 16 "types of divisors". A precomputed PD-table (PD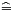 partial division) of size 128x16 contains the results for all possibilities and q0 is computed by table-look-up.
partial division) of size 128x16 contains the results for all possibilities and q0 is computed by table-look-up.
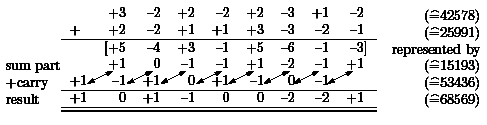
The radix-4 SRT divider uses some more tricks. One of them is the following. Having chosen q0 we have to compute the new remainder which equals 4 . (r-q0.d ) (the shift in the school method is replaced by a multiplication by 4, since we work with radix-4 numbers). We have seen that the computation of q0.d is easy, since q0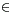 {-2,-1, 0, +1, +2}. In order to simplify the subtraction the remainder is represented as sum of two numbers (another redundant representation) allowing the use of CSA gates for subtraction (see Section 5).
{-2,-1, 0, +1, +2}. In order to simplify the subtraction the remainder is represented as sum of two numbers (another redundant representation) allowing the use of CSA gates for subtraction (see Section 5).
Although the design of this radix-4 SRT divider is complicated, there is no real obstacle to discuss it in high school. Moreover, it is important to see not only toy examples but the design of a part of a processor which has been sold many million times. The Pentium bug is discussed in the next section.
We finish this section with a small example:
+001.101001 : 1.001101or
r=1.101001 and d=1.001101.
The Pentium divider only considers the prefixes r'=+001.101 (or 13/8) and d'=1.001 (or 9/8). This implies 4d' = 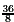 <
< 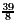 = 3r'. Hence, one may expect that q0=2 is allowed as the first piece of the quotient (as radix-4 representation). However, it is possible that the dividend is r"=13/8 and the divisor contains many ones following 1.001. The divisor may be close to d"=
= 3r'. Hence, one may expect that q0=2 is allowed as the first piece of the quotient (as radix-4 representation). However, it is possible that the dividend is r"=13/8 and the divisor contains many ones following 1.001. The divisor may be close to d"=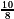 . However, 4d"=
. However, 4d"=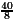 >
>![]() = 3r". Hence, knowing only r' and d' the result q0=2 is forbidden. In our example r=
= 3r". Hence, knowing only r' and d' the result q0=2 is forbidden. In our example r=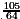 , d=
, d=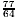 and 4d=
and 4d=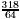 <
<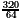 =3r and q0=2 would be allowed. However, the entry +2 is forbidden as an entry of the PD-table in row +001.101 and column 1.001. This shows that the task to compute legal PD-entries is not easy.
=3r and q0=2 would be allowed. However, the entry +2 is forbidden as an entry of the PD-table in row +001.101 and column 1.001. This shows that the task to compute legal PD-entries is not easy.
Indeed, it is not obvious that there is at least one legal input for each PD-entry. However, the division method works and a PD-table with legal entries exists.
7. Some aspects of the verification of circuits
Products sold by computer science oriented companies should have some guaranteed quality, just like products from other engineering disciplines. The main aspect is correctness. Verification is the task to prove formally that the realization R has the same input-output-behavior as the specification S, i.e., we ask whether R S. The problem is not trivial, since R and S may be quite different solutions of the same problem, i.e., the school method and Newton's method for division.
S. The problem is not trivial, since R and S may be quite different solutions of the same problem, i.e., the school method and Newton's method for division.
Indeed, it is known since a long time that the general verification problem for software products is undecidable while the problem for hardware products is coNP-complete. It is not necessary to define these notions. The information that these problems are provably difficult is enough.
For the problem of circuit verification we have to distinguish three subproblems:
- the proof that a specific algorithm is correct, this is possible for all the algorithms presented in this paper,
- the proof that the realized gate list describes a circuit computing the same function as represented by the circuit given as specification, this is the core problem of circuit verification,
- the proof that there is no production fault, a problem which is treated by circuit testing.
Because of the hardness of the problem, we cannot hope for an algorithm solving all problem instances efficiently. Hence, we are looking for heuristic algorithms which efficiently solve many of the problem instances which have to be solved in real world applications. The nowadays most successful approach is to transform the circuits S and R into other representation types S' and R' respectively such that S S' and R
S' and R R' are guaranteed. The new representation types should have the property that S'
R' are guaranteed. The new representation types should have the property that S' R' can be checked efficiently. However it may happen that S' is exponentially larger than S and/or R' is exponentially larger than R. Then our verification approach fails. The state-of-the-art representation type for this approach is the representation by ordered binary decision diagrams (OBDDs, see Wegener (2000)). Nevertheless, this approach is not strong enough to verify multipliers and dividers (even for 16-bit numbers). However, the Pentium divider is an iterative algorithm and it is possible to verify the correctness of one round of this approach. The famous Pentium bug could have been found with such an approach.
R' can be checked efficiently. However it may happen that S' is exponentially larger than S and/or R' is exponentially larger than R. Then our verification approach fails. The state-of-the-art representation type for this approach is the representation by ordered binary decision diagrams (OBDDs, see Wegener (2000)). Nevertheless, this approach is not strong enough to verify multipliers and dividers (even for 16-bit numbers). However, the Pentium divider is an iterative algorithm and it is possible to verify the correctness of one round of this approach. The famous Pentium bug could have been found with such an approach.
There are many possibilities to obtain an incorrect gate list from a correct algorithm. The Pentium bug was caused by some faulty entries in the PD-table. This table has 211 entries and extensive testing should consider many more than 211 entries. However, the bad entries were extreme cases where 3r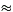 8d. Since the Pentium divider starts with numbers 1
8d. Since the Pentium divider starts with numbers 1 r<2 and 1
r<2 and 1 d<2 there are only few inputs where these "extreme entries" have to be used implying that even intensive testing had a good chance of missing the bug. This leads to the conclusion that verification is essential, a conclusion necessary to be taught very early in computer science courses.
d<2 there are only few inputs where these "extreme entries" have to be used implying that even intensive testing had a good chance of missing the bug. This leads to the conclusion that verification is essential, a conclusion necessary to be taught very early in computer science courses.
8. Some didactic aspects
As an example of teaching the hardware for basic arithmetic operations we have chosen the prefix algorithm. The reader will see that it is not impossible to teach such a subject in a high school class. Some general didactic remarks will follow.
8.1 How to teach the prefix algorithm
Within a series of lessons about recursive and especially divide-and-conquer algorithms the prefix algorithm seems to be a quite good excursion. It is possible to teach the design and the analysis of an algorithm for an important and non-trivial problem.
8.2 Didactical aims
The learners- know a divide-and-conquer and, therefore, recursive algorithm in order to solve the prefix problem,
- develop and formulate an algorithm and describe it graphically,
- are able to analyze depth and complexity of simple recursive algorithms, and
- see the advantage in time of a hardware-based realization of a parallel algorithm.
8.3 Methodical suggestions
MotivationThe true motivation is the calculation of the carry bits within the Ladner-Fischer adder. However, this motivation is difficult to teach. Moreover, one has to interrupt the teaching of the Ladner-Fischer adder and the learners are in danger to lose the thread. Moreover, they see the prefix problem for the first time with a quite difficult and abstract associative operator.
Therefore, we suggest to introduce the prefix problem before starting with the Ladner-Fischer adder and to introduce it for situations where the associative operator is the simple addition of numbers. To motivate the prefix problem for "+" we have two suggestions. The management of a company has for each day of the last year the information, how many pairs of shoes have been sold and how many pairs of shoes have been delivered by the producers. Now they are interested in the stock at each day of the last year. Hence, they are faced with a prefix problem. The same is true for the soccer fan who has a list of the results of the last championship. Now she or he likes to produce the league situations after each round. For each team three prefix problems have to be solved: points won, goals scored, and goals scored by the opponents.
Definition and a first solution of the special prefix problem
We define the special prefix problem and then describe how the learners will start with the naive algorithm and how they will find (supported by the teacher) better algorithms.
The special prefix problem is to calculate all pi=xi+...+x0, 0 i
i n-1. We have described above how we can motivate this problem in different ways. The next step is to introduce graphical representations of algorithms where
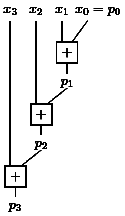
n-1. We have described above how we can motivate this problem in different ways. The next step is to introduce graphical representations of algorithms where ![]() is a black box for the addition of two numbers. We have no doubt that each learner is able to present an algorithm for the special prefix problem. At least, the naive algorithm, computing pi=xi+pi-1 sequentially is too easy to be missed. Figure 9 is the graphical representation of this algorithm and Figure 10 a simple abstraction. This abstraction is useful, since it abstracts already from the special operator.
is a black box for the addition of two numbers. We have no doubt that each learner is able to present an algorithm for the special prefix problem. At least, the naive algorithm, computing pi=xi+pi-1 sequentially is too easy to be missed. Figure 9 is the graphical representation of this algorithm and Figure 10 a simple abstraction. This abstraction is useful, since it abstracts already from the special operator.
 |
 |
 |
| Figure 9: The naive algorithm for the special prefix problem. | Figure 10: An abstract form of the naive algorithm. |
Development of a better algorithm
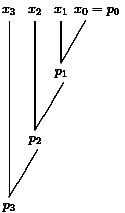
Divide-and-conquer algorithms (like the conditional sum adder, see A1) often partition the problem into two subproblems of the same type, solve the two subproblems recursively and then combine these solutions with some extra work to a solution of the problem. This should be known. Here our purpose is to reduce the depth of the inherently sequential naive algorithm. We start with the first non-trivial case n=4. Then the two problems have a size of n=2 and the only way to solve each of them is obvious. How can we combine the intermediate results z1=x3+x2 and p1=x1+x0? Each learner will "see" that p3=z1+p1 (see Figure 11). However, the result p2 is still missing. Again the learner will "see" that p2=x2+p1. The whole solution is shown in Figure 12.
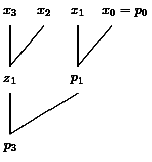 |
 |
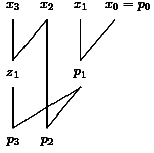 |
| Figure 11: First attempt of an improvement. | Figure 12: Real improvement. |
The learners can analyze the result. The depth is reduced from 3 to 2, while the size has been increased from 3 to 4. Now the learners are prepared to solve the problem for n=8 (see Figure 13).
|
Figure 13: Solution for n = 8. |
The learners draw two solutions for n = 4, one for x7,...,x4, the other one for x3,...,x0. Then the outputs p0,...,p3 are computed and a discussion should show that pi=qi+p3 for i>3.
Formulation of the algorithm
Based on the experiences for n=4 and n=8 small teams of learners are asked to generalize these experiences and to formulate an algorithm for general n=2k. The proposals are discussed leading to the following algorithm.
Algorithm
Analysis of the algorithm
The description of the algorithm simplifies the analysis. Recursive algorithms lead to recursive equations for the resources. Let D(n) and C(n) be the depth and the size, respectively. By definition of the algorithm, D(1)=0 and C(1)=0. In Step 1, we have two subproblems of size n/2. Hence, the size equals 2.C(n/2). However, the problems are solved in parallel implying that the depth is only D(n/2). In Step 2, we have n/2 operations which are performed in parallel, i.e., in depth 1. Hence,
Improved algorithm
The algorithm presented in Section 3 reduces the size from (1/2)n log n to linear at the cost of doubling the depth. This can be taught in an advanced course. The main idea is to reduce the input size from n to n/2 by constructing pairs. Then the problem is solved recursively with this reduced input size. However, we only obtain the results p2i with an even index. This again can be deduced easily from graphical representations. The last idea is that all p2i+1=x2i+1=p2i can be computed in parallel.
Additional methodical proposals
A course on prefix algorithms allows many discussions between the learners and the teacher. The learners have a good chance to produce results and it is even likely that they produce different solutions. The solutions can be presented graphically for small n and the teacher can control whether all learners can apply the algorithms. Afterwards, a discussion shows the advantages and disadvantages of the different algorithms.
This all is possible on a blackboard or with an overhead projector. However, the projector supports the power of copying the algorithm for the right half of the input to work also on the left half of the input. Moreover, a last slide shows how the solutions of the subproblems are stuck together.
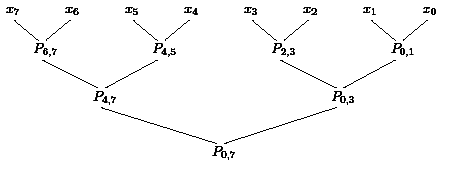
If only few recursive algorithms have been taught before, a role play can show what is really going on. For n=8, seven learners or players are involved. Their tables can be arranged like a complete binary tree with eight leaves (see Figure 14).
|
Figure 14: Arrangement of players in the role play. |
Now we see an iterative version of the recursive solution. Player Pi,j is responsible for solving the problem for xj,...,xi. Player P0,7 partitions the problems and passes the subproblems to the children players which do the same until problems of size 1 have reached the leaves. These problems are recognized as solved. In the second round, players stick the solutions for the subproblems together (they apply Step 2 of the algorithm) and pass the solution to the parent. Finally, P0,7 holds the solution of the problem.
Duration
Recursion is a difficult subject. Roberts (1987) (as cited by Baumann (1996)) reports: "At the first introduction [of the recursion] the learners often respond with a dislike against this idea, so as if they are confronted with magic and not with a new programming method." Hence, learners have to see a series of recursive algorithms to be convinced of its value. The first recursive algorithm needs a lot of time, but the time for each further algorithm is reduced. However, we estimate that four lessons are necessary.
Evaluation
On the average, the time to teach all prefix algorithms is six lessons. However, the learners solve an important problem (it is important for itself and a subprogram of the Ladner-Fischer adder) and they see different applications of recursion. No special prerequisites are necessary and in each lesson fundamentals of computer science are taught.
8.4. Didactical remarks
Many didactical remarks have been mentioned in the previous sections. Here we repeat the most important ones and add some general ones.It is our strong belief that the investigation of the hardware realization of the basic arithmetic operations is a worthwhile subject of high school courses in computer science. The reasons are manifold.
First of all, the subject is without any reasonable doubt fundamental. No special and long-winded motivation is necessary. The learner will accept that each processor needs an ALU (arithmetic logic unit) and has routines to do arithmetics. However, she or he may have the objection that the subject is too simple to be considered. We all know the school methods and most of the learners believe that these methods are the only or at least the only reasonable methods for the arithmetic operations. The first message therefore is fundamental. Good solutions for humans may be no good solutions for computers and vice versa. Computers use other algorithms for the basic arithmetic operations than humans do. Problems that seem to be solved for ever turn out to be of essential nowadays importance. Everybody has to overcome her or his strong belief that she or he knows "everything" about arithmetics. This is an experience which should train the learner to doubt in other real world situations whether the obvious way is the only one or the best one. This is one of the few situations where computer science courses lead to insights useful in the everyday life.
The subject combines computer science disciplines like computer architecture, hardware design, analysis of algorithms, data structures, parallelization, and complexity. It is easy to formalize the problems, since circuits, circuit size and circuit depth can be introduced easily. It is an advantage that circuits are graphs (with some extra information) and have a graphical and concrete realization. Nevertheless, it is necessary to stress the fact that one has to be sure about the aims of optimization before one starts to look for a good or optimal solution. It is perhaps the first time that the learner is confronted with a multi-objective optimization problem, a situation which is the typical one in real world optimization. A solution which only optimizes size or depth cannot be used as a practical solution. Nevertheless, it may be the starting point for further investigations. There is another motivating aspect. After having heard that the dividers of modern computers work differently from the school method, an interested learner likes to see the solution realized in processors she or he knows (like the Pentium processors). The fact that such big companies produce bugs leading to a financial disaster (450 million $) should make the subject thrilling. This directly leads to the often ignored subject of verification. We strongly believe that high school courses in computer science have to confront the learner with the verification problem. The early discussion of this subject is necessary to train computer scientists feeling responsible for the correctness of their products and to produce clients who do not accept that hardware and especially software products are faulty and that the client has to pay for improvements. Altogether, the learning goals are not restricted to the core of the problem. There are several much more general aspects in teaching the considered subject.
However, the presented solutions contain many issues and methods which are typical in computer science teaching. First, the learner gets skilled in algorithmic thinking. It is a highly creative job to design algorithms which differ from the mainstream ideas. Nobody expects that one can avoid the bit-by-bit multiplication in multipliers. The learner sees that one can beat (sometimes) obvious bounds - like the n2 size bound for multipliers.
However, surprising new solutions contain well-known ideas and design principles. The learner is trained to apply the following techniques: modularization, divide-and-conquer, dynamic programming, table-look-up, approximation, and rounding. Some algorithms are recursive and others are iterative ones. It is good to see that the naive application of recursive algorithms leads to a computational overhead, since the same subproblems are solved again and again. An analysis of the resources spent by algorithms turns out to be necessary to decide which solution is the better one. The subject contains many algorithms whose analysis is easy but there are also some advanced problems. It turns out that it would be much harder to perform an exact analysis and that it is often sufficient to perform an asymptotic analysis (with some control of the constants).
We point out some special learning goals:
- the characterization of bit positions as E-, P-, and G-position (for adders) is an useful abstraction, the learner gets even new insights about addition,
- the prefix problem is an abstraction of many problems (given the daily turnover compute the turnover of the last i days for all integers i), the problem has a simple solution with a good size and a good depth,
- if algorithm A is superior to algorithm B if the input size is large enough but algorithm B is good for short inputs, one should think about algorithms combining the advantages of A and B,
- mathematicians are interested in the convergence of sequences, computer scientists have to be interested in the rate of convergence,
- one has to distinguish between the correctness proof for algorithms, the verification of gate lists, and the testing of chips after production,
- redundant number representations are the core of many hardware solutions.
Although the subject has a mathematical flavor, only a few mathematical tools are necessary: computing with logarithms, computing derivatives of simple functions (for Newton's method), composition of functions (for the Ladner-Fischer adder), the value of finite arithmetic and geometric series, and proofs by induction. The learner sees applications of these fundamental mathematical tools. Besides this it is useful to know something about trees, in particular, balanced binary trees and asymptotic estimates, i.e., the growth order of runtimes expressed in the O-notation.
Because of the mathematical origin of the problems the subject has an interdisciplinary flavor. Some people may get for the first time an access to the "world of numbers". Another interdisciplinary aspect is the bridge to engineering disciplines. Hardware realization also is an issue of electrical engineering. In any case, a message is that computer science cannot be reduced to programming. Moreover, the considered solutions do not depend on the technology (as long as we investigate electronic components) and methods do not become antiquated quickly (the Pentium divider is based on an idea from the sixties).
We hope that we have convinced the reader that the subject is not too difficult to be taught in high school courses, although we admit that the learner has to struggle in order to follow all arguments. We believe that nowadays computer science courses are no challenge for the talented learner. Here she or he is faced with such a challenge. Nevertheless, any interested learner can follow the course. It is an advantage that even those who are very preoccupied with computers do not have an advantage for this subject. The teacher can decide to omit some of the algorithms. In any case, the subject shows by examples how scientists solve problems. Hence, the discussion of the hardware realization of the arithmetic operations is a preparatory course for scientific learning at universities.
The teacher may use different teaching forms. She or he may ask for ideas and discuss ideas presented by learners. In some situations it will be necessary that the teacher presents a method. However, the analysis can be worked out in a dialogue between the teacher and the learners. The learner can visualize the solution for small n in detail which supports her or his understanding. Teams of learners can cooperate. The information flow of algorithms can be illustrated by role plays where learners or groups of learners are responsible for certain modules or levels of recursion. Kersting (1999) has worked out a course in detail which is suitable for the German school system.
9. Conclusions
We have argued why the hardware realization of the basic arithmetic operations is at least an interesting but perhaps even a thrilling subject for computer science courses in high schools. Many learning goals can be achieved teaching this subject. Experiments have to prove that our proposals are realistic.
References
- Baumann, R. (1966). Didaktik der Informatik. Klett.
- Kersting, P. (1999). Hardwarerealisierungen für die Grundrechenarten und ihre mögliche Behandlung im Unterricht. Staatsexamensarbeit. Univ. Dortmund.
- Wegener, I. (1987). The complexity of Boolean functions. Wiley-Teubner.
- Wegener, I. (1996). Effiziente Algorithmen für grundlegende Funktionen. Teubner.
- Wegener, I. (2000). Branching programs and binary decision diagrams - theory and applications. SIAM-Monographs on Discrete Mathematics and Applications.
Appendix
Here we present some further algorithms for the arithmetic operations.
A1. The conditional sum adder
We have seen in Section 3 on adders that the only problem is the computation of carries. The new idea is the following. If we do not know the carry, we compute the sum for a carry and without a carry. If we finally know the value of the carry bit, we select the correct result. Selection (or if-then-else) is a basic operation realizing the statement
(a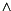 b)
b) 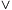 (
(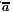
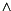 c)
c)
where 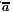 = NOT(a). We assume that
= NOT(a). We assume that 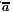
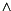 c can be realized as a basic binary operation. Then a selection circuit has size 3 and depth 2. A recursive description of the CS-method is the following.
c can be realized as a basic binary operation. Then a selection circuit has size 3 and depth 2. A recursive description of the CS-method is the following.
Base of recursion: The addition of two bits without a carry can be performed by a half adder. The addition of two bits and a carry bit 1 can be done by c = x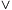 y and s = x
y and s = x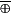 y (
y (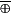 = NEXOR). The size for both computations is 4 and the depth equals 1.
= NEXOR). The size for both computations is 4 and the depth equals 1.
The general task is to compute the sum s of x, y and a bit c. We partition x = (x", x') and y = (y", y') into two blocks of equal size. Then we apply the algorithm recursively to compute in parallel
| - the sum of x', y', and c,
- the sum of x", y", and 0, - the sum of x", y", and 1. |
The last n/2 bits of the first result are equal to the last n/2 bits of the final result. Let d be the carry of the first result. The leading n/2+1 bits of s are equal to the second result, if d=0, and they are equal to the third result, if d=1. Hence, n/2+1 selections are sufficient to compute the final result. These selections can be performed in parallel. Again the recursion depth equals log n. Including the base of the recursion we obtain DEPTHCS(n)=2 log n+1. Hence, we obtain an adder of very small depth. The size of the last step equals 3(n/2+1) and we have to solve 3 problems of input length n/2. This leads to 32 problems of length n/4, 33 problems of length n/8, ..., 3k problems of length n/2k = 1. Since k = log n,
3k=3log n=nlog 3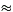 n1.58.
n1.58.
The learner should get in trouble with this result. A problem of length 1 is the problem to compute the sum of xi, yi, and c. Hence, the number of different problems equals 2n and our algorithm solves nlog 3 of these problems. This implies that the algorithm solves the same problem again and again. This effect can be observed by considering explicitly two steps of the recursion. Hence, we learn that recursion supports the description of ideas and algorithms. However, in order to obtain an efficient implementation it may be necessary to consider an iterative version. In other words: divide-and-conquer has to be replaced by dynamic programming. The CS-method is a good example to teach algorithmic paradigms.
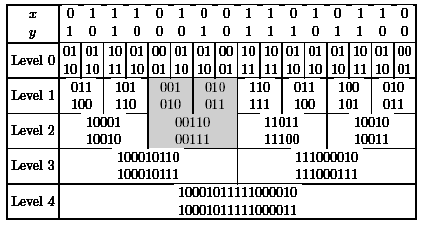
The iterative version can be described as follows. Level 0 contains the base of recursion as before. Level t considers the partition of x and y into n/2t blocks of length 2t each. The sum of the corresponding blocks with and without carry is computed using the results of the two subblocks from the previous level using the method explained in the recursive version of the algorithm. This sounds complicated. It is easy to explain the algorithm using an example (see Figure 15).
|
Figure 15: The CS method for n = 16. |
The first line of each level contains the results for the value 0 of the carry bit and the second line contains the result for a carry bit equal to 1. We consider the part of the computation which is marked in Figure 15. We have to compute (0,1,0,0)+(0,0,1,0)+c for c=0 and c=1. The last two bits are known, since we have computed (0,0)+(1,0)+c on the last level. Hence, we are interested in the leading three bits. We also know the results for (0,1)+(0,0)+c', c'=0 and c'=1, from the last level. Here c' is the carry from the previous block and c' depends on c. Since the leading bits of the results 010 and 011 (last level, previous block) are 0, we have in both cases c' = 0 and get in both cases the result of (1,0)+(0,0)+0. This iterative tableau also simplifies the analysis. Level 0 has depth 1 and each other level has depth 2 (the two lines of each block can be computed in parallel).
The exact size equals
SIZECS(n)=3n log n+10n-6.
It is not necessary to perform this exact computation. The size of level 0 equals 4n. On each other level we compute more than 2n bits and at most 3n bits. Less than one half of the bits but at least a third of these bits are for free. Each other bit needs one selection operation whose size is 3. Hence, we obtain an upper bound of 6n and a lower bound of 3n for each of the other log n levels. Hence, the size is of the order n log n and not comparable with the linear size of the Ladner-Fischer method.
A2. A size-efficient multiplexer
We design a multiplier using much less than n2 gates. It is a divide-and-conquer approach where x=(x'',x') and y=(y'',y') are partitioned into two blocks of equal size (almost equal size if n is odd). Then (let | x| denote the values of the n-bit number x)
= | x''| . | y''| . 2n + (| x''| . | y'| + | x'| . | y''|) . 2n/2 + | x'| . | y'|.
This leads to four subproblems of length n/2 and some additions. Multiplications by fixed powers of 2 are shifts and do not need hardware cost. However, we have gained nothing. We obtain 4 subproblems of length n/2. On the next level of recursion we have 42 subproblems of length n/22, then 43 subproblems of length n/23 and, finally, 4k subproblems of length n/2k=1 if n=2k. A subproblem of length 1 can be solved with one AND-gate. The number of these subproblems equals
4k = 22k = (2k)2 = n2
and we need n2 gates for the subproblems of length 1. Furthermore, we have to perform the various additions. Now it is essential to continue thinking about this approach and not to give up. Karatsuba and Ofman made the following simple but ingenious observation:
| x"| . | y'| + | x'| . | y"| = (| x"| + | x'|) . (| y"| + | y'|) - (| x"| . | y"| + | x'| . | y'|).
This observation can be verified in a second. This leads to the following recursive algorithm:
| - compute p1 = | x"| . | y"| by recursion,
- compute p2 = | x'| . | y'| by recursion, - compute s1 = p1 + p2, - compute s2 = | x"| + | x'|, - compute s3 = | y"| + | y'|, - compute p3 = p1 . p2 by recursion, - compute the result as p3 - s1 (the subtraction is easy, since it is known that the result is not negative). |
| - 4 A/S(n) (addition/subtraction of numbers of a bit length bounded above by n) which can be performed in size 4.c.n for some constant c,
- 3.4 A/S(n/2) on level 1 of the recursion whose cost is bounded by 3.4.c.n/2, - 32.4 A/S(n/22) on level 2 of the recursion, cost 32.4.c.n/22, ... - 3m.4 A/S(n/2m) on level m of the recursion, cost 3m.4.c.n/2m. |
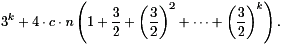
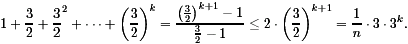
We know that 3k=nlog 3 n1.58 (see the discussion on the conditional sum adder). Hence, the simplified analysis leads to an upper bound of the circuit size of nlog 3+12.c.nlog 3=
n1.58 (see the discussion on the conditional sum adder). Hence, the simplified analysis leads to an upper bound of the circuit size of nlog 3+12.c.nlog 3= (nlog 3). The growth order is also correct without the simplification. Hence, (KO = Karatsuba and Ofman method)
(nlog 3). The growth order is also correct without the simplification. Hence, (KO = Karatsuba and Ofman method)
SIZEKO(n)= (nlog 3).
(nlog 3).
A3. Radix-4 representations of numbers
A number in radix-4 representation of length n is a vector x=(xn-1,..., x0) where xi {-3, -2, -1, 0, +1, +2, +3}. Its radix-4 value equals
{-3, -2, -1, 0, +1, +2, +3}. Its radix-4 value equals
xn-14n-1+...+x14+x0.
(Remark: In order to control the length of the numbers one has to know that the result of a computation is contained in {0,..., 4n}. Then one can perform the computation mod(4n+1). This is a background information not necessary for teaching.) It is easy to transform a binary number into a radix-4 representation. It is sufficient to consider bit pairs, e.g., 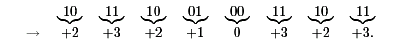
The reverse transformation leads to a subtraction if we group the positive and the negative components separately, e.g.,
| +3 | -2 | +1 | -1 | -3 | -2 | 0 | +2 | ||
 |
11 | 00 | 01 | 00 | 00 | 00 | 00 | 10 | |
| - | 00 | 10 | 00 | 01 | 11 | 10 | 00 | 00 |
The multiplication by (- 1) is obvious and therefore, subtractions can be replaced by additions. The crucial step is the addition of two numbers in radix-4 representation in constant depth. This seems to be difficult, since carries are possible, e.g., 3+3=6 and even 3+1=4 leading to forbidden numbers. The solution again is simple and ingenious.
In the first step we perform an add(2 2)-step which seems to be no progress. However, we use the redundancy of the representation to choose the sum parts (no longer sum bits) and the carries in such a way that the next add(2
2)-step which seems to be no progress. However, we use the redundancy of the representation to choose the sum parts (no longer sum bits) and the carries in such a way that the next add(2![]() 2)-step guarantees that all carries are 0. Hence, two add(2
2)-step guarantees that all carries are 0. Hence, two add(2 2)-steps performed in a well chosen way realize an add(2
2)-steps performed in a well chosen way realize an add(2 1)-step. Figure 16 describes the choice of the sum parts and the carries. The sum s of two numbers contained in { -3, -2, -1, 0, +1, +2, +3} is contained in {-6,..., +6}.
1)-step. Figure 16 describes the choice of the sum parts and the carries. The sum s of two numbers contained in { -3, -2, -1, 0, +1, +2, +3} is contained in {-6,..., +6}.
|
Figure 16: The addition of one position of radix-4 numbers. |
The surprising and crucial decision is to represent +3 as (-1).40+(+1).41 and not in the more natural way (+3).40+(0).41. The representation of -3 is chosen in the analogous way. The effect of this choice is that all sum parts are contained in {-2, -1, 0, +1, +2} and all carries are contained in {-1, 0, +1}. Hence, in the next step we have to add a sum part and a carry leading to a value in { -3, -2, -1, 0, +1, +2, +3} implying that the sum can be represented without carry. Figure 17 shows an example.
|
Figure 17: The addition of radix-4 numbers. |
Hence, all hardware implementations can work with radix-4 representations implying that additions and subtractions (and also multiplications by powers of 2, i.e., shifts for the usual binary representation) can be performed in constant depth. Only the final result has to be transformed with a Ladner-Fischer subtraction into a binary representation. This implies that the multipliers using the Karatsuba and Ofman algorithm or Schönhage and Strassen algorithm or any mixed algorithm can be realized in logarithmic depth.
A4. Newton's method for division
We describe Newton's method in a general form. Let f :
 be strictly decreasing (f'(x)<0) and convex (f"(x)>0), f(a)>0, and f(b)<0 (see Figure 18). Then f has a unique zero z*
be strictly decreasing (f'(x)<0) and convex (f"(x)>0), f(a)>0, and f(b)<0 (see Figure 18). Then f has a unique zero z*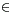 [a,b] which can be approximated by Newton's method in the following way. Let f(zi)>0, let T be the tangent touching f at zi, and let zi+1 be chosen such that T(zi+1)=0. Thenzi<zi+1<z* and we have obtained a better approximation of z*.
[a,b] which can be approximated by Newton's method in the following way. Let f(zi)>0, let T be the tangent touching f at zi, and let zi+1 be chosen such that T(zi+1)=0. Thenzi<zi+1<z* and we have obtained a better approximation of z*.
|
Figure 18: Newton's method for convex functions. |
Division is the composition of computing the inverse and multiplication. Hence, we consider the computation of the inverse z-1 of z. This is the unique zero of the strictly decreasing, convex function f(x)=x-1-z. Simple calculation shows that
zi+1=2zi-z.zi2.
The general formula contains a division and we may give up, since we look for a division algorithm. However, the special formula for the special function f only contains shifts, multiplications and subtractions. Let 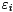 =z-1-zi be the error of our approximation. We may assume that (after some appropriate shifts) 1/2
=z-1-zi be the error of our approximation. We may assume that (after some appropriate shifts) 1/2 z<1 and 1<z-1
z<1 and 1<z-1 2. Then z0=1 is an appropriate first approximation such that
2. Then z0=1 is an appropriate first approximation such that 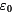
 1. A simple three-lines-computation (see Wegener(1996)) proves, that
1. A simple three-lines-computation (see Wegener(1996)) proves, that ![]()
 1/2 and
1/2 and ![]() <
<![]() , i.e., the number of correct bits is doubled in each round. Hence,
, i.e., the number of correct bits is doubled in each round. Hence,  log n
log n +1 rounds are sufficient to obtain n correct bits.
+1 rounds are sufficient to obtain n correct bits.
Here one can discuss some numerical aspects. If z and zi are n-bit numbers, then z.z2i is a (3n)-bit number and after some rounds we work with very long numbers. The solution is to round the intermediate results in such a way that the property zi<z* is guaranteed. Working with numbers of bit length 2n the number of rounds has to be increased by a small amount and is still O(log n). Then we have O(log n) sequential shifts, multiplications and subtractions. Hence, the depth is O(log2n) and the size is by a factor of O(log n) larger than the size of the multiplier which is used. Quite careful estimations show that three rounds with bit length 6 are sufficient to obtain an error of less than 1/4. Afterwards  log n
log n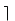 rounds are sufficient to decrease the error to 2-n even if we work in the ith round with numbers of bit length 2i+1+3. This is a subject which should not be considered in detail. The final result of the detailed investigations is that the bit length in the first rounds is small enough such that the size of the resulting divider is for all considered multipliers only by a constant factor larger than the n-bit multiplier of the considered type. The depth is O(log2n).
rounds are sufficient to decrease the error to 2-n even if we work in the ith round with numbers of bit length 2i+1+3. This is a subject which should not be considered in detail. The final result of the detailed investigations is that the bit length in the first rounds is small enough such that the size of the resulting divider is for all considered multipliers only by a constant factor larger than the n-bit multiplier of the considered type. The depth is O(log2n).
A5. The IBM method for division
The IBM method again is based on a simple idea. We are interested in approximating z-1 where 1/2 z<1. Let x=1-z. Then 0<x
z<1. Let x=1-z. Then 0<x 1/2 and
1/2 and
The last step is the essential one. Since x 1/2, x2k+1 is very small (if k is not too small) and 1-x2k+1 can be approximated by 1. We are left with 2k multiplications
1/2, x2k+1 is very small (if k is not too small) and 1-x2k+1 can be approximated by 1. We are left with 2k multiplications
| - x2, x4,..., x2k by iterative squaring,
- the computation of 1+x2m from x2m is for free, since x2m<1, - the computation of the product of all (1 + x2m), 0 m k. |
Again it is difficult to find such a method and it is easy to understand it. The IBM method also has a numerical aspect. It is sufficient to choose k= log(n+2)
log(n+2) -1 and to work with s-bit numbers for s=n+4
-1 and to work with s-bit numbers for s=n+4 log k
log k .
.
Comments